Random nature of decay - constant decay probability for a given nucleus

Use of activity, A = λN
Questions may be set which require students to use
A = A0e−λt
Questions may also involve use of molar mass or the Avogadro constant
Half-life and decay constant and their determination from graphical decay data including decay curves and log graphs;
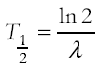
Applications, e.g. relevance to storage of waste radioactive materials; radioactive dating
|
Recall that radioactive activity is:
 spontaneous (probability of a decay cannot be changed by changing pressure/temperature etc.) spontaneous (probability of a decay cannot be changed by changing pressure/temperature etc.)
 random - direction that ray is emitted or which nucleus will decay when - is impossible to say! But when dealing with large numbers of atoms the mathematics of probability can be employed. random - direction that ray is emitted or which nucleus will decay when - is impossible to say! But when dealing with large numbers of atoms the mathematics of probability can be employed.
 Recall that radioactive decay is an exponential process therefore probability is applicable! Recall that radioactive decay is an exponential process therefore probability is applicable!
You should be able to
 sketch a graph of number of nuclei against time (marking on multiples of No and T (half) to show th exponential relationship) sketch a graph of number of nuclei against time (marking on multiples of No and T (half) to show th exponential relationship)
 recall that the rate of decay recall that the rate of decay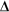 N/ N/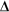 t (or Activity of the sample) is proportional to the number of atoms of the radioisotope present in the sample. t (or Activity of the sample) is proportional to the number of atoms of the radioisotope present in the sample.
 Recall that the decay constant ( Recall that the decay constant (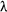 ) is the constant of proportionality between activity and sample size. It gives a measure of the probability that a particular nucleus in a sample will decay in a given time. It has units of time-1.(The negative sign before it is because the number present decreases with time - so that would lead to a negative constant!) ) is the constant of proportionality between activity and sample size. It gives a measure of the probability that a particular nucleus in a sample will decay in a given time. It has units of time-1.(The negative sign before it is because the number present decreases with time - so that would lead to a negative constant!)
 recall that the half life of a radioisotope is the time taken for half of the radioactive nuclei of that isotope substance in a sample to decay. This is constant for any given isotope. The units are those of time. recall that the half life of a radioisotope is the time taken for half of the radioactive nuclei of that isotope substance in a sample to decay. This is constant for any given isotope. The units are those of time.
 appreciate the variation in natural half-lifes from nanoseconds to millions of years and the affect this has on uses and safeguards when disposing of waste. appreciate the variation in natural half-lifes from nanoseconds to millions of years and the affect this has on uses and safeguards when disposing of waste.
 know about carbon dating. know about carbon dating.
Now try some questions - I suggest Q4, Q6, Q8 and Q9 from this link 
MS 1.3, 3.10, 3.11 / PS 3.1, 3.2 Investigate the decay equation using a variety of approaches (including the use of experimental data, dice simulations etc) and a variety of analytical methods. |


