Topic Menu

Cyber-chess a chess instruction site

Module 6: Particles and medical physics

6.2 Electric fields

6.2.1

Point and spherical charges

(a) electric fields are due to charges

(b) modelling a uniformly charged sphere as a point charge at its centre

(c) electric field lines to map electric fields

(d) electric field strength;

E = F/Q

6.2.2

Coulomb's law

(a) Coulomb's law;

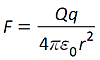
for the force between two point charges

You will also require knowledge of section 3.2

(b) electric field strength

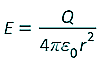
for a point charge

(c) similarities and differences between the gravitational field of a point mass and the electric field of a point charge

 

 

 

Link to section 5.4

(d) the concept of electric fields as being one of a number of forms of field giving rise to a force.

6.2.3

Uniform electric field

(a) uniform electric field strength;

E = V/d

Learners will also require knowledge of 3.1, 3.2 and 3.3

(b) parallel plate capacitor; permittivity;

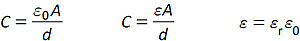
Learners are not expected to know why the relative permittivity ε≥ 1

(c) motion of charged particles in a uniform electric field.

6.2.4

Electric potential and energy

(a) electric potential at a point as the work done in bringing unit positive charge from infinity to the point;

electric potential is zero at infinity

  

(b) electric potential

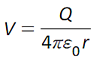
at a distance r from a point charge;

changes in electric potential

  

(c) capacitance

C = 4πε0R

for an isolated sphere

Derivation of this is expected from the equation for electric potential and Q = VC.

  

(d) force–distance graph for a point or spherical charge;

work done is area under graph.

  
 

(e) electric potential energy

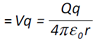
a distance r from a point charge Q.