| 3.6.2.1 Thermal energy transfer |
Internal energy is the sum of the randomly distributed kinetic energies and potential energies of the particles in a body.
The internal energy Q of a system is increased when energy is transferred to it by heating or when work is done on it (and vice versa), eg a qualitative treatment of the first law of thermodynamics.
Appreciation that during a change of state the potential energies of the particle ensemble are changing but not the kinetic energies.
Calculations involving transfer of energy.
For a change of temperature '∆θ' energy transfer ∆Q:
∆Q = mc ∆θ
where 'c' is specific heat capacity and 'm' is mass of substance.
Calculations including continuous flow.
For a change of state the energy transfer ∆Q:
∆Q = ml
where 'l' is the specific latent heat and 'm' is mass of substance changing state .
 SHC and Latent Heat Questions SHC and Latent Heat Questions
|
Internal energy (sometimes called the random thermal energy) of a substance is the sum of kinetic energy and potential energy.
- Potential energy is due to the interaction of neighbouring particles, this is therefore very significant in solids and liquids but less so in gases.
- Kinetic energy is due to the movement of the particles in the substance.
You should be able to define the specific heat capacity of a substance as being the quantity of energy required to raise the temperature of 1kg of the substance by 1K.
You should realize that the biggest changes in temperature of a given mass of a substance will occur in those that have low specific heat capacities - because it doesn't take much energy for them to get hotter!
You should be able to define specific latent heat as the energy required to change the state of 1 kg of the substance.
You should be able to understand what is happening to the particles in a substance when heat is added to it or taken away if the substance is remote from its melting or boiling point it will change temperature (getting hotter or colder) as the particles vibrate faster or slower on absorbing the heat energy - the kinetic energy component changes significantly the potential energy component is virtually the same..
The amount of heat energy required to make a temperature change of 1K will depend on the mass of the substance (the more you have the more energy you will need, natch!) and what it is - some structures react to heat input more dramatically than others (this is indicated in the SHC 'c' of the substance) - low 'c' substances have particles that are easier to 'vibrate'!
If the substance is at its boiling/melting point the energy given/taken away will not be used to get hotter or colder. It will be used to change state.
- If absorbed (given to the substance) it will not make the particles vibrate any faster, but will make them freer from each other.
- If being taken away, again it will not change the vibration of the particles but rather will make them more structured - less free - and change their state to do that.
So when latent heat is involved we are looking at the change of potential energy not kinetic energy.
You should be able to do calculations involving heat being given and/or taken away. Remember to add up all of the components that have been 'given energy' and all of those that have 'given energy away' and equate them in an exchange of heat problem. |
| 3.6.2.2 Ideal gases |
Gas laws as experimental relationships between p, V, T and the mass of the gas.
Concept of absolute zero of temperature.
Ideal gas equation (also called the 'Equation of State'):
pV = nRT for n moles
pV = NkT for N molecules.
Work done = p∆V
Avogadro constant NA
Molar gas constant R,
Boltzmann constant k
Molar mass and molecular mass. |
Required practical 8: Investigation of Boyle's law (constant temperature) and Charles’s law (constant pressure) for a gas
- recall the properties of an ideal gas
- know that the nearest we have to an ideal gas is helium remote from its boiling point and at low pressure.
- use the equations to do calculations
- know that T must be in Kelvin!
- know that a mole is the Avogadro number of particles
- appreciate where absolute zero (-273oC becoming 0K) comes from (extrapolation of p/T and V/T graphs) |
| 3.6.2.3 Molecular kinetic theory model |
Brownian motion as evidence for existence of atoms.
Explanation of relationships between p, V and T in terms of a simple molecular model.
Students should understand that the gas laws are empirical in nature whereas the kinetic theory model arises from theory.
Assumptions leading to
pV = 1/3Nm (crms) 2
including derivation of the equation and calculations. (A simple algebraic approach involving conservation of momentum is required).
Appreciation that for an ideal gas internal energy is kinetic energy of the atoms.
Use of average molecular kinetic energy equation
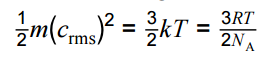
Appreciation of how knowledge and understanding of the behaviour of a gas has changed over time.
 Kinetic Theory Questions Kinetic Theory Questions
|
Gas Laws: Boyle's Law and Charles Law
- be able to sketch graphs of p against V, p against T, V against T
- know that NA is the number of particles in a mole of gas
- you have very few derivations to learn! Make sure you know this one well! You must learn the assumptions too and use words to explain how to derive it!
- understand how temperature of particles relates to their kinetic energy and mean square speed.
- internal energy of an ideal gas is only kinetic - it has (by definition no potential energy!)
- internal energy (sometimes called the random thermal energy) of a gas is the sum of kinetic energy and potential energy but the potential energy is so tiny that it can often be ignored. Potential energy is due to the interaction of neighbouring particles, this is therefore very significant in solids and liquids
- average molecular kinetic energy for a gas sample is directly proportional to absolute temperature in an ideal gas. (sketch the graph from the equation!)
- note that the Boltzmann constant k is simply R/NA
- the average molecular kinetic energy equation is for a (to find the total energy for a gas sample you would have to multiply by nNA) |


