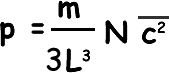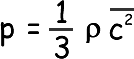The kinetic theory of gases (derivation of the equation relating pressure to mean square speed and density) Let’s try to explain experimentally some observed properties of gases by considering the motion of the particles (molecules or atoms) which they are made up of. To do that we need to make a number of assumptions:
Some of these assumptions run through the entire analysis; others are used more specifically.
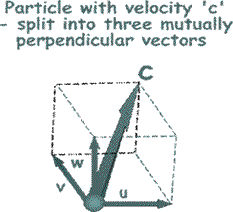
To make the mathematical treatment easier to understand we need to break all of those random velocities into components that are mutually at right angles to each other. (See the illustration on the right). That will make it easier later on to add them all up or average them!
Consider a fixed mass of gas enclosed in a cubical container of side L. Let each particle of the gas have mass m and let there be N particles
Let’s start with just looking at one of the millions of particles in the gas.
Look at the diagram - the particle it represents is one of millions, but we will forget those for the moment! The diagram shows the u component of a single particle moving towards the wall shaded in grey. We will call this particle 1
When the particle hits the wall it will bounce back with the same speed but in the opposite direction (because kinetic energy is conseved – the collision being elastic!). The x-component of momentum will then be -mu1 The change in momentum - The particle has to travel a distance 2L (from the shaded wall to the opposite face and back again) before it next collides with the shaded wall again. Now, velocity = distance/time so
so the rate of change of momentum due to a collision with a wall will be:
By Newton's second law, the rate of change of momentum is equal to force, so mu12/L is the force exerted on the particle by the wall during the collision. By Newton's third law, the particle exerts an equal but oppositely directed force on the wall, and so we can say that: The force on the wall during the collision = mu12/L Now it isn’t only one particle that hits the wall – there are N particles so their x-components of velocity are going to be u1, u2,…. uN The total force, F, will therefore be = mu12/L + mu22/L + mu32/L….. + muN2/L F = m/ L ( u12+ u22+ u32... + uN2) Now, pressure on that wall will be force/contact area = F/A, but A = L 2 Therefore pressure on the wall – the pressure of the gas p = m/ L 3 ( u12+ u22+ u32... + uN2) We can work out the mean square velocity is the x direction from this:
So now we know that the total pressure due to the u-components of the velocities of the particles will be:
By Pythagoras c 2 = u 2 + v 2 + w 2 So, it follows that this is true for the mean square velocities also.
Since there are large numbers of molecules and they are moving randomly the mean square components are equal to each other (random movement means there is no preferred direction). We can therefore say that
We can now replace our mean square velocity component with one related to the mean square velocity itself.
Now, density is mass/volume, Nm is the total mass of gas and L3 is the volume; we can therefore say that:
|
Follow me...
|


 We need to think about the velocity of the particles.
We need to think about the velocity of the particles. 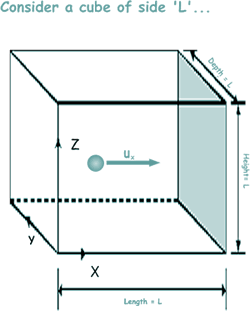

 So far we have only looked at one of the component velocities (the 'u' component) . It is now time to look at the other two ('w' and 'v') and to add them into the equation.
So far we have only looked at one of the component velocities (the 'u' component) . It is now time to look at the other two ('w' and 'v') and to add them into the equation.