Topic Menu

Cyber-chess a chess instruction site

Academic Applications - Uses of Nuclear Radiation

The most common and accepted method of 'absolute geologic dating' (establishment of actual age) is based on the natural radioactivity of certain minerals found in rocks. As the rate of radioactive decay of any particular isotope is known, the age of a specimen can be worked out from the ratio of the remaining isotope and its decay product.

Dating of Igneous Rocks (Using Uranium Content)

Geologists use this method to date igneous rock samples. If you look carefully at the half-lives of isotopes in the Uranium Series you appreciate that the uranium has a much longer half-life than any of the others.

So, by comparing the proportion of Uranium in the rock to the proportion of lead produced by its decay you can work out how many half-lives it has been decaying.

Then by using the half-life of Uranium you can work out the time involved.

Percentage of Uranium
Percentage of Lead
Ratio of Uranium to Lead
Age (millions of years)
Initial Value
100.00%
0.00%
1:0
0
After one half-life
50.00%
50.00%
1:1
4,500
After two half-lives
25.00%
75.00%
1:3
9,000
After three half-lives
12.50%
87.50%
1:7
13,500
After four half-lives
6.25%
93.75%
1:15
18,000

Dating of Ancient Artefacts (Carbon Dating)

Carbon dating measures the remaining amount of the radioactive isotope carbon-14 in organic matter. It can be used to date specimens as old as 35,000 years.

During its lifetime a biological entity (plant or animal) takes an active part in the carbon cycle and it contains the same proportion of the isotope as the atmosphere does (about one ten millionth of the carbon is carbon-14).

The death of an organism terminates the incorporation of this isotope into the fabric of the entity. From the time of death onwards the proportion of carbon-14 in the dead orgamism decreases as it decays into nitrogen.

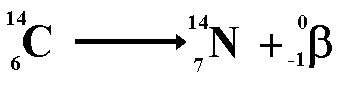
By calculating the ratio of C-14 to total carbon in a sample of the artefact it is possible to work out its age. The half-life of carbon-14 is 5,600 years.

E.g.

C-14 in total carbon
Age (years)
Initial Value 1 part in 10 million
0
After one half-life 0.5 parts in 10 million 
5,600
After two half-lives 0.25 parts in 10 million 
11,200
After three half-lives 0.125 parts in 10 million
16,800
After four half-lives 0.0625 parts in 10 million
22,400