Young's Slits - Evidence that light behaves like a wave

Historical Background

The nature of light had been argued about for centuries.

In 1803, the corpuscular theory was widely held as being true but an English physicist named Thomas Young demonstrated the interference of light. Now that couldn't be explained by particles!

Young reasoned that if light was made of waves some type of interaction would occur when two light waves met. Diffracting light through a slingle slit he produced coherent waves. These 'in step waves' were then directed onto a double slit - effectively producing two coherent light sources. After being diffracted, the light that is recombined by interference the constructive and destructive interference produced a series of bright and dark fringes along the length of a screen.

Young's conclusions were not widely accepted at the time, primarily because of the overwhelming belief in the particle theory. In addition to his observations on light interference, Young postulated that light of different colors was composed of waves having different lengths, a fundamental concept that is widely accepted today.(In contrast, the particle theory advocates envisioned that various colors were derived from particles having either different masses or traveling at different speeds)..

A simple experiment to observe Young's Fringes

To observe interference of light, we need a coherent source.

If we illuminate two closely spaced parallel slits (double slits) using a suitable light source the two slits act as two coherent sources of light waves, meaning the slits emit light waves with a constant phase difference and the same frequency.

In Young's day he performed the experiment using a candle flame!

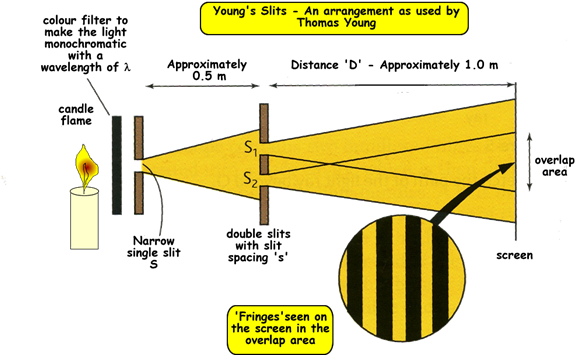
Light Source - must be coherent

Nowadays we can use a bulb instead of a candle – for safety reasons! But in order to get monochromatic light from it we would have to use a filter like Young and filters absorb a lot of the light energy. It would be better to just have a monochromatic source of light.

A sodium lamp gives out yellow light of two wavelengths that are very close to each other – virtually monochromatic - temporally coherent. No filter is needed. (A single slit would still be needed though, to make two spacially coherent sources from the monochromatic source.

Or we could use a laser - that is totally coherent - no filter and no single slit would be needed if the aperture of the laser was small enough.

Single slit - needed for all light sources other than the laser

The purpose of the single slit is to make the source of waves that hit the double slit arrangement as coherent as possible. The waves from a single point source would be spacially coherent, so the single slit creates a point source in the arrangement. Then both slits are hit by waves from this single point source.

If the single slit is too wide, the dark fringes of the double slit pattern become narrower than the bright fringes, and contrast is lost between the dark and the bright fringes. You therefore need to aim to have the slit narrow enough to produce equally spaced ones but not so narrow that the overall intensity is too low.

Double slits - to produce Young's Slits pattern of fringes

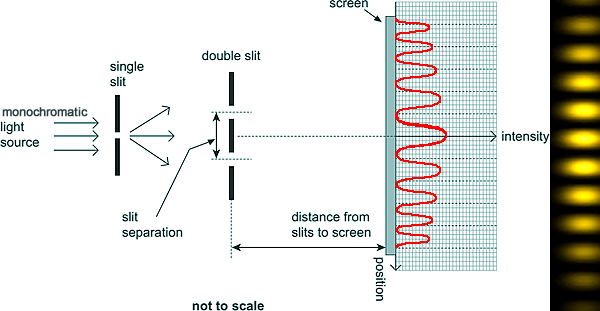
In the above arrangement the single slit improves the spatial coherence of the light from the source - it is already improved in temporal coherence by being monochromatic. The intensity of the light allowed throug would be too low to perform this experiment in a well lit room. You would need to have the blinds pulled down and be limited as to how long you could make 'D'.

Using a laser means you can dispense with the single slit altogether and have a brighter coherent source and you can make 'D' really long.

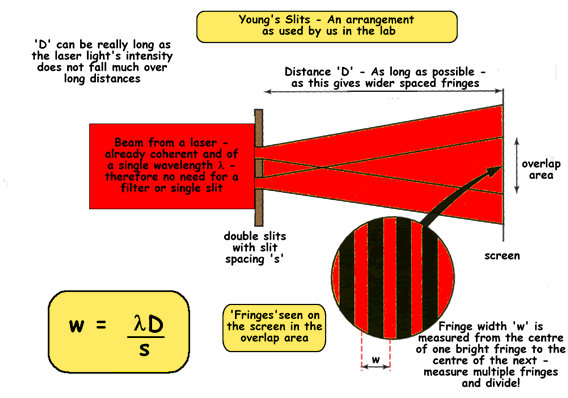
As a result of this experiment alternate bright and dark fringes, referred to as Young's fringes,can be seen on a white screen placed where the diffracted light from the double slits overlaps and produces an interference pattern.

The fringes are evenly spaced and parallel to the double slits.

In practical experiments we only use the fringes that are in the central maximum of the single slit envelope. The intensity of the fringes in the centre of this band is virtually uniform.

 

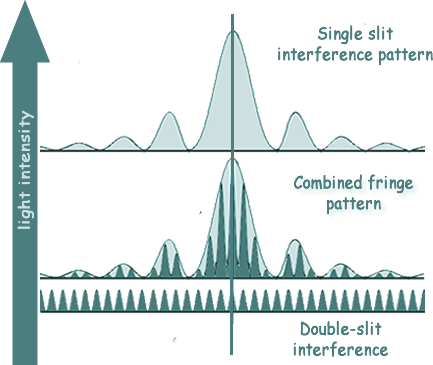The fringes are formed due to interference of light from the two slits:

Where a bright fringe is formed, the light from one slit reinforces the light from the other slit. In other words, the light waves from each slit arrive in phase with each other.

Where a dark fringe is formed, the light from one slit cancels the light from the other slit. In other words, the light waves from the two slits arrive 180° out of phase.

-----------------------------

When you perform this experiment you will notice some dimming in the fringes as you travel out from the centre.

This is because the regular light-dark bands are superimposed on the light pattern from the single slit. The intensity pattern you observe is a combination of both the single-slit diffraction pattern and the double slit interference pattern.

The amplitude of the diffraction pattern is said to modulate the interference pattern. The diffraction pattern for a single slit acts like a viewing screen for the interference pattern. The photo at the top of this section above is taken from the central maximum area of a display - it is this area you have to use to take measurements from.

Fringe Separation

The distance from the centre of a bright fringe to the centre of the next bright fringe is called the fringe separation ‘w’. This depends on the slit spacing ‘s’ and the distance ‘D’ from the slits to the screen.

From the equation we can see that the fringes become more widely spaced if:

the distance D from the slits to the screen is increased,

the wavelength X of the light used is increased,

the slit spacing, s, is reduced.

The theory of the double slits equation

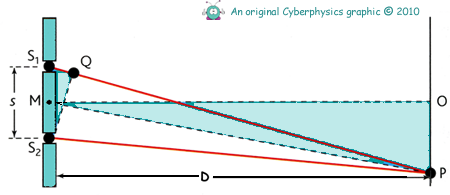
Consider the two slits S^₁ and S₂

At a point P on the screen where the fringes are observed, light emitted from S_l arrives later than light from S₂ emitted at the same time. This is because the distance S₁P is greater than the distance S₂P.

The difference between distances S₁P and S₂P is referred to as the path difference.

For reinforcement at P, the path difference S₁P - S₂P = mλ, where m   = 0, 1, 2, etc.
Therefore, light emitted simultaneously from S₁ and S₂ arrives in phase at P if reinforcement occurs at P.

For cancellation at P, the path difference S₁P - S₂P = (m + ½ )λ, where m = 0, 1, 2, etc.
Therefore, light emitted simultaneously from S₁ and S₂ arrives at P out of phase by 180° if cancellation occurs at P.

A point Q along line S₁P has been marked such that QP = S₂P. therefore the path difference S₁P - S₂P is represented by the distance S₁Q.

Consider triangles S₁S₂Q and MOP, where M is the midpoint between the two slits and O is the midpoint of the central bright fringe of the pattern. The two triangles are very nearly similar in shape, as angles S₁S₂Q and PMO are equal and the long sides of each triangle are of almost equal length.

Therefore

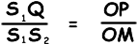
If P is the mth bright fringe from the centre (where m = 0, 1, 2, etc), then S₁Q = mX and OP = mw, where w is the distance between centres of adjacent bright fringes. Also, OM = distance D and S₁S₂ = slit spacing s.

Therefore,

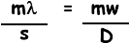
You can cancel the m and then you get:

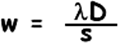
By measuring the slit spacing, s, the fringe separation, w, and the slit-screen distance D, the wavelength λ of the light used can be calculated.

The formula is valid only if the fringe separation, w, is much less than the distance D from the slits to the screen.

This condition is to ensure that the triangles S₁S₂Q and MOP are very nearly similar in shape.

 

Try these multiple choice questions.