Topic Menu

Cyber-chess a chess instruction site

RMS - root mean square speed

RMS stands for the root mean square speed.

This is the square root of the average (mean) of all of the square of the speeds of individual particles in a gas.

The mean square speed is written thus:
The root mean square speed is written thus:

'c' is used as the symbol for the speed of a particle

the 'bar over the top' means the mean (average) of all of those squared speeds.

The mean square speed is different from the mean speed squared - careful with how you express yourself in answers!

Suppose we take eight molecules with speeds of 300m/s, 400 m/s, 400 m/s, 500 m/s, 600 m/s 600 m/s, 700 m/s and 900 m/s.

Let us calculate their mean speed squared and their mean square speed.

Their mean speed squared is simply that - find the mean speed and square it! Such a figure has no physical significance to us as physicists - it is purely a mathematical exercise.

Try it!

To find their mean speed simply add up the speeds and divide by eight - and then square your answer.

You should get  302 500 m2/s2.

 

Now let's find their mean square speed:

Square each speed, add them together and divide by eight.

You will get 330 500 m2/s2.

Now this value is meaningful to physicists because it relates to the kinetic energy of the average molecule.... and that relates to temperature

 

Why would we want to find the mean square speed?

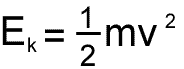
Temperature is related to the kinetic energy of particles, and the kinetic energy of a particle relates to the square of the speed of a particle - therefore, if we want to look at average kinetic energy (and hence average temperature) we have to look at the mean of the squared speeds of the molecules in the sample.

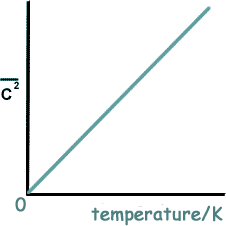
So, if you take the individual speeds of a group of particles - square each one - add them up and then divide by the number of particles you are dealing with, you get the mean square speed - and that gives an indication of absolute temperature.

At 0K the mean square speed would be 0m/s.

At 200K it would be double whatever it was at 100K.

The mean square speed is proportional to absolute temperature.

Why would we want to find the root mean square speed?

If we take the square root of the mean square speed we get the RMS speed.

We have then found the speed of the particle that has the same temperature as the average temperature of all of the particles.

It is the speed of the 'particle of average temperature' within a gas.This is very different from the average speed... or most probable speed!

 

Now let's do some practice questions to familiarise yourself with the RMS speed.