When to ignore the current through a voltmeter The total current that flows through a parallel arrangement depends on the voltage drop across it. Voltmeters are connected in parallel with components and should be chosen for the task only if they have very high resistance compared to the resistance of the component they are 'measuring the voltage' across. When this is the case they make very little difference to the total resistance of the arrangement.
Three resistors are connected in parallel (2.0 Ω, 5.0 Ω and 20 Ω) – calculate the equivalent resistance of the arrangement.
1 /R TOTAL = 1/2 + 1/5 + 1/20 = 0.75 So, R TOTAL = 1/0.75 = 1.3 ( or 4/ 3) Ω (2 s.f. because the resistances were given to that standard) (Note that this result is smaller than the smallest resistance in the arrangement! This is always the case – useful tip!!)
1 /R TOTAL = 1/2 + 1/5 + 1/20 + 1/3000 = 0.75033 (working to so many figures purely to illustrate the point!) So, R TOTAL = 1/0.75033 = 1.3Ω (the same value as before the voltmeter was added to the circuit - it makes no measurable difference) The voltmeter does not interfere in a measurable manner with the resistance of the arrangement - it therefore does not interfere with the voltage distribution across the circuit. You would need very sensitive meters to notice the difference. The higher the resistance of the voltmeter the less it interferes with the circuit it is measuring potential differences in. The current that passes through the arrangement will be greatest in the resistor of lowest value. Let us suppose that a voltage of 6.0 V was applied across our arrangement. We can work out the current through the whole arrangement using V = IR: V = IR I = V / R = 6.0 / 1.33 (here a calculated value is put in at one more sig fig than we must quote to – necessary for accuracy – always work to one more figure!) = 4.5 A This current is split into the four branches of the circuit. Using the values of each of the resistors in turn with the p.d. across them we can work out how much current goes into each strand.
V = IR I = V / R = 6.0 / 2.0 = 3.0 A
V = I R I = V / R = 6.0 / 5.0 = 1.2 A
V = IR I= V / R = 6.0 / 20 = 0.30 A
V =IR I = V / R = 6.0 / 3000 = 0.002 A Sum of currents = 0.002 A + 0.30A + 1.2 A + 3.0 A = 4.502 A = 4.5 A (2 sig figs) – we can ignore the current draw by the voltmeter as it is so small
Always read the question carefully. If it says a ‘high resistance voltmeter…’ it means ignore the current drawn by it and assume it does not affect the resistance of the circuit. BUT if it gives you the resistance you need to do calculations with that resistance to find out what it reads.
Because the resistance of the voltmeter is ‘high’ (compared to the resistances in the circuit) we can ignore it and confidently say that the reading on it will be 3.0V. The two parallel 30 Ω resistors would have a resistance of 15 Ω in that arrangement, forming only a third of the resistance in the strand. The voltmeter would therefore read 3V. BUT if the value of R was 3000 Ω then we would have a very different situation. The parallel arrangement would then be of three 3000 Ω resistors (equivalent to 1000 Ω ) and the voltmeter would only read a quarter of the terminal voltage 2.25V (2.3V on the dial). If the voltmeter was replaced with a very high resistance (sometimes called high impedance) electronic meter (like a multimeter) then the reading on it would be 3V as before – its resistance would not have to be included in the calculation.
|
Follow me...
|


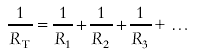
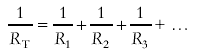
 In this circuit let us suppose the value of V is 9 volts, the value of R is 30 Ω and the voltmeter has a resistance of 3000 Ω .
In this circuit let us suppose the value of V is 9 volts, the value of R is 30 Ω and the voltmeter has a resistance of 3000 Ω .  Basic terms
Basic terms



