Section 3.4.5 - Magnetic effects of currents - click here for an interactive site
 - magnetism questions in a 'flip-book' for you to try - magnetism questions in a 'flip-book' for you to try |
 - electromagnetic induction questions in a 'flip-book' for you to try - electromagnetic induction questions in a 'flip-book' for you to try |
|
| |
Syllabus Extract |
You should be able to: |
| 3.7.5.1 Magnetic flux density |
Force on a current carrying
wire in a magnetic field
F = BIl (field perpendicular to current)
Fleming's Left hand Rule
Magnetic flux density B and definition of the tesla T
|
Compare and contrast electric and gravitational fields - good table on pg 94. |
| 3.7.5.2 Moving charges in a magnetic field |
Motion of charged particles in a magnetic field Force on charged particles in a magnetic field F = BQv (field perpendicular to velocity) Circular path of particles; application, e.g. charged particles in a cyclotron
|
Use Fleming's left hand rule to establish force at right angles to motion.
- Relate this to the condition for circular motion.
- Equate expression for centripetal force to BQv.
- Establish effect on radius of orbit if B, m or accelerating voltage change.
Practical: Could show crossed fields experiment here to find e/m. Value obtained is of the right order of magnitude.
MS 4.3 Convert between 2D representations and 3D situations.
|
| 3.7.5.3 Magnetic flux and flux linkage |
Magnetic flux density B, flux Φ and Flux Linkage NΦ
Magnetic flux defined by Φ = BA, where B is normal to A.
Flux linkage as NΦ, where N is the number of turns cutting the flux Φ.
Flux and flux linkage passing through a rectangular coil rotated in a magnetic field:
flux linkage N = BAN cosθ where θ is the angle between the normal to the plane of the coil and the
magnetic field. = BAN cosθ where θ is the angle between the normal to the plane of the coil and the
magnetic field. |
Define B and relate the two terms using a diagram, this will also explain the value of when B is not perpendicular to the area concerned ( = BA cos θ )
Required practical 11: Investigate, using a search coil and oscilloscope, the effect on magnetic flux linkage of varying the angle between a search coil and magnetic field direction. |
| 3.7.5.4 Electromagnetic induction |
Simple experimental phenomena.
Faraday's and Lenz's laws
For a flux change at a uniform rate 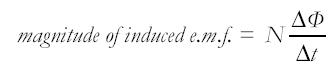
Magnitude of induced EMF = rate of change of flux linkage.
Applications such as a moving straight conductor, e.g. p.d. between wing-tips of aircraft in flight
Emf induced in a coil rotating uniformly in a magnetic field:
ε = BAN ω sin ωt
|
Recall Faraday's Law: that the magnitude of the induced EMF in a circuit is directlt proportional to the rate of change of flux linkage (or to the rate of cutting of magnetic flux). Recall Lenz's Law: that the direction of the induced EMF is such that the current which it causes to flow opposes the change which is producing it. Know that the induced EMF is therefore:  directly proportional to the number of turns of wire directly proportional to the number of turns of wire
 proportional to the rate of cutting of flux (how fast the flux lines atr cut by the wire) proportional to the rate of cutting of flux (how fast the flux lines atr cut by the wire)
 produced in such a way as to make a current flow that has a magnetic field that opposes the field of the one causing the induction. produced in such a way as to make a current flow that has a magnetic field that opposes the field of the one causing the induction.
|
3.7.5.5 Alternating currents |
Sinusoidal voltages and currents only; root mean square, peak and peak-to-peak values, for sinusoidal waveforms:
Alternating currents
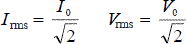
Application to calculation of mains electricity peak and peak-to-peak voltage values
|
- understand that power dissipation by an AC signal of given RMS signal is the same as the DC signal of the same numerical value
sketch a sinusoidal trace when given peak (amplitude, peak to peak or RMS) current/voltage and the frequency
- sketch the trace for mains voltage (recalling 230V rms is 330V peak and the frequency is 50Hz)
- perform calculations changing rms into peak and vice versa
|
|
Oscilloscope
Use of an oscilloscope as a d.c. and a.c. voltmeter, to measure time intervals and frequencies, and to display waveforms.
No details of the structure of the instrument is required but familiarity with the operation of the controls is expected. |
- set up the oscilloscope to investigate an electrical signal
- determine the amplitude and frequency of a signal (AC/DC) as displayed on an oscilloscope
- describe 'how' to use an oscilloscope - what to connect where and what dials to turn to make the reading easier and more accurate. |
| 3.7.5.6 The operation of a transformer |
The operation of a transformer;
The transformer equation
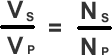
Transformer efficiency = Is Vs / Ip Vp
Causes of inefficiency of a transformer.
Transmission of electrical power at high voltage including calculations of power loss in transmission lines. |
MS 0.3 / AT b, h Investigate relationships between currents, voltages and numbers of coils in transformers. |


