In DC voltage there is a steady potential difference between the ends of the wire, but an AC voltage causes the potential difference to change in a sinusoidal manner.This results in a different type of current in a wire submitted to a DC voltage than it experiences if an AC voltage is applied to it.
With DC voltage application the charge flow is steady in one direction - with AC the charges oscillate - first being pulled in one direction and then in the other....
D.C. Power Supply
A D.C. power supply has a fixed positive terminal (usually coloured red or marked with '+ve') and a fixed negative terminal (usually coloured black or marked with '-ve'.) The positive terminal is a fixed electrical potential higher than the one marked negative.
Electrical cells or batteries supply DC power - power packs from mains electrical generators only give a rectified d.c. supply - the AC changes to DC via circuitry.
If the potential difference between two terminals is constant it supplies a direct voltage and that makes a direct current - a steady current - flow in a circuit.
The current is related to the potential difference across a resistor by the equation:
V = IR
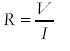(expressed in this form on the AQA data sheet)
The power dissipated in the resistor (the electrical energy transferred into heat energy in the resistor) is given by
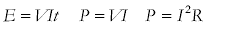
Power is the product of the voltage across the resistor and the current passing through it.
The power is the energy transferred (in joules) each second
Remember that 1W = 1J/s
This is a steady transfer of energy from electrical energy to heat in the resistor.
A.C. Power Supply
An A.C. power supply has two identical terminals (usually coloured yellow).
The potential difference between the terminals varies sinusoidally.
In effect the one terminal changes from being maximum potential to minimum potential and back to maximum again while the other does the opposite - starting at minimum potential, going to maximum and back to minimum again. So in effect they alternate between being positive and negative.
Electrical generators supply AC power.
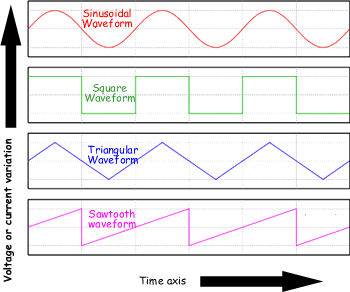When the potential difference between the terminals varies with time it supplies a waveform such as those on the right. The varying voltage makes the current through the circuit vary too. The current is still related to the potential difference across a resistor by the equation:
V = IR
but as that p.d. is varying the current will vary too.
The most common variation of waveform is the alternating current. The electrical generators that work well with transformers (i.e. the ones we use in a mains electrical supply) produce a sinusoidal waveform.
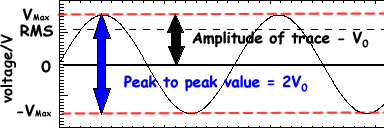
The voltage increases from zero to a peak value and then decreases down through zero to a negative of that peak value and the it increases back to zero again before the whole process begins again.
This variation occurs 50 times a second in the UK - 50 Hz frequency (in the US it is 60 times a second - 60 Hz frequency).
An equation that describes the variation with time is:
V = V0 sin(2πf)t
where
- V is the voltage,
- f is the frequency and
- V0 is the amplitude (maximum voltage)
.
This variation means that the current through a resistor will also vary sinusoidally:
I = I0 sin(2πf)t
where
- I is the current,
- f is the frequency and
- I0 is the amplitude (maximum current)
The power dissipated will also vary but with a sine squared variation.
- When the current and voltage are zero no energy will be changing
- When the current and voltage are a maximum there will be maximum energy dissipation.
- When the current and voltage are negative maxima the power will also be that positive maximum (as the product of two negatives is a positive!)
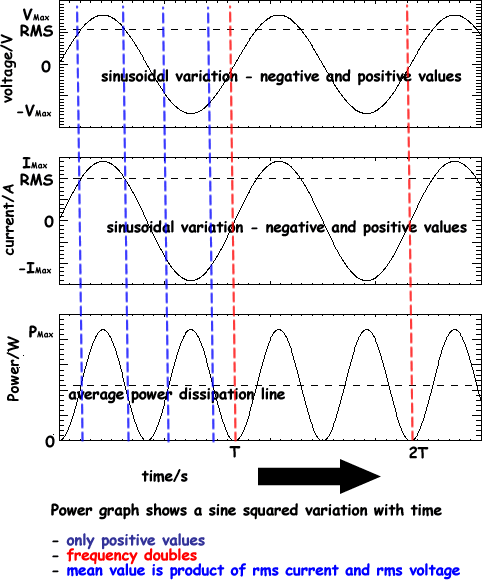
The voltage and current that multiply together to give average power are the RMS (root mean square) values.
You can see this on the diagram above.
At A level you no longer have to do the maths to derive the relationship between average power and RMS - but you ARE expected to know that an alternating supply of any RMS voltage will produce the same average power dissipation in a resistor as a DC voltage of that value would produce.
RMS values of alternating power supplies are the value that gets quoted to consumers (e.g. UK power is 230V RMS). That is because we need to work out the average power dissipation from the supply.
It is simple to find out the peak value from an RMS value and vice versa.
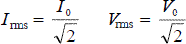
and you need to realise that for a resistor:
V = IR
so
V0 = I0R
and
VRMS = IRMSR
About this site
Note it is a sine equation - leading to a sinusoidal waveform
