Topic Menu

Cyber-chess a chess instruction site

Circular Motion

Q1.

(a) Derive an expression to show that for satellites in a circular orbit T2 ∝ r3 where T is the period of orbit and r is the radius of the orbit.

[2 marks]

(b) Pluto is a dwarf planet.

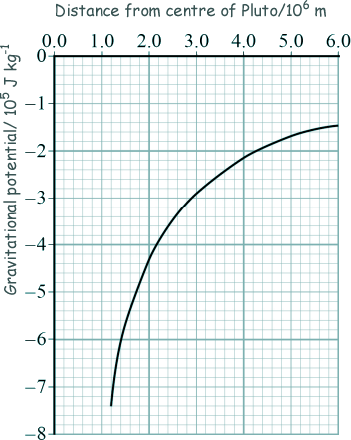
The mean orbital radius of Pluto around the Sun is 5.91 × 109 km compared to a mean orbital radius of 1.50 × 108 km for the Earth.

Calculate in years the orbital period of Pluto.

[2 marks]

(c) A small mass released from rest just above the surface of Pluto has an acceleration of 0.617 m s−2.

Assume Pluto has no atmosphere that could provide any resistance to motion.

Calculate the mass of Pluto.

Give your answer to an appropriate number of significant figures.

radius of Pluto = 1.19 × 106 m

[3 marks]

(d) The graph shows the variation in gravitational potential with distance from the centre of Pluto for points at and above its surface.

A meteorite hits Pluto and ejects a lump of ice from the surface that travels vertically at an initial speed of 1400 m s−1 .

Determine whether this lump of ice can escape from Pluto.

[3 marks]

(10 marks total)