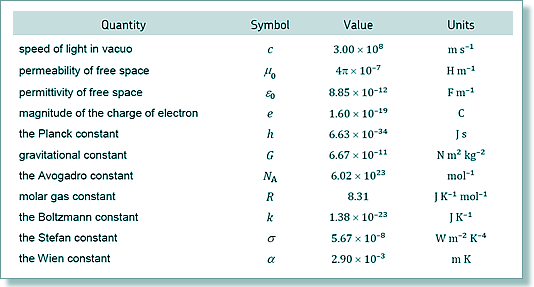
Nuclear Fission Q1. What is the binding energy of the nucleus Use the following data:
Q2. The fission of one nucleus of uranium 235 releases 200 MeV of energy. What is the value of this energy in J? 200 MeV = 200 x 106 eV = 200 x 106 x 1.6 x 10-19 J = 3.2 x 10-11 J
Q3. The mass of the nuclear fuel in a nuclear reactor decreases at a rate of 1.2 × 10–5 kg per hour. Assuming 100% efficiency in the reactor what is the power output of the reactor?
1.2 × 10–5 kg per hour = 1.2 × 10–5/602 kg per second = 1.2 × 10–5/(1.661 x 10-27x 602) u per second = 931.3 x 1.2 × 10–5/(1.661 x 10-27x 602) MeV per second = 931.3 x 12/(1.661 x 10-27x 602) eV per second = 1.6 x 10-19 x 931.3 x 12/(1.661 x 10-27x 602) J per second = 3.0 x 108 W = 3.0 x 102 MW
Q4. The moderator in a nuclear reactor is sometimes made of graphite. What is the purpose of the graphite?
Q5. Which line, A to D, in the table gives a combination of materials that is commonly used for moderating, controlling and shielding respectively in a nuclear reactor?
Q6. Which one of the following statements is not true about the control rods used in a nuclear reactor?
Q7. A thermal nuclear reactor is shut down by inserting the control rods fully into the core. Which line, A to D, shows correctly the effect of this action on the fission neutrons in the reactor?
Q8. For a nuclear reactor in which the fission rate is constant, which one of the following statements is correct?
Q9. Artificial radioactive nuclides are manufactured by placing naturally-occurring nuclides in a nuclear reactor. They are made radioactive in the reactor as a consequence of bombardment by
Q10. In a thermal reactor, induced fission is caused by the
Q11. Why is a moderator required in a thermal nuclear reactor?
Q12. The nuclear fuel, which provides the power output in a nuclear reactor, decreases in mass at a rate of 6.0 × 10–6 kg per hour. What is the maximum possible power output of the reactor?
6.0 × 10–6 kg is equivalent to 6.0 × 10–6/1.661 × 10–27 u = 931.5 x 6.0 × 10–6/1.661 × 10–27MeV therefore in 1 second the energy output is 931.5 x 6.0 × 10–6/(1.661 × 10–27 x 602) MeV = 9.347 x 1020 MeV = 9.347 x 1026 eV
energy each second = 9.347 x 1026 x 1.60 x 10-19 J energy each second = 1.5 x 108 J That happens each second so power output = 150 MW - choice C
|
Follow me...
|