Topic Menu

Cyber-chess a chess instruction site

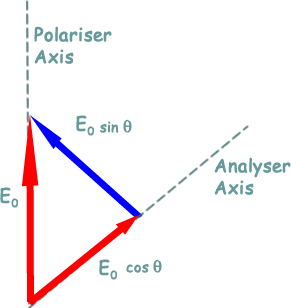
Malus's Law

Malus' law: It = Io cos2 θ

where θ is the angle between the polarization direction of the incident light and the transmission axis of the polarizer.

----------------------------------------------------------

When unpolarised light is passsed through a polarising filter its intensity is halved and only light parallel to the grid within the polarising filter is allowed through.

The transmitted light then has the same axis of polarisation as the filter that polarised it. It is then perfectly plane polarised light.

---------------------------------------

When perfectly plane polarized light is incident on an analyzer, the intensity It of the light transmitted by the analyzer is directly proportional to the square of the cosine of angle between the transmission axes of the analyzer and the polarizer.

i.e

It ∝cos2θ

  • Let the angle between the transmission axes of the analyzer and the polarizer be θ.
  • The completely plane polarized light form the polarizer hits the analyzer at right angles.
  • If E0 is the amplitude of the electric vector transmitted by the polarizer, then intensity I0 of the light incident on the analyzer is I ∝ E02
  • Let us resolve electric field vector into two perpendicular components i.e E0 cos θ and E0 sin θ.

The analyzer can transmit only the component which is parallel to its transmission axis ( i.e E0 cos θ ) and the component E0sinθ will be absorbed by the analyser. Therefore, the intensity It of light transmitted by the analyzer is:

It ∝ ( E0 x cos θ )2

It / I0 = ( E0 x cos θ )2 / E02 = cos2 θ

so, It = I0 x cos2θ

∴ It ∝ cos2 θ.

  • When θ = 0° ( or 180° ), It = I0 cos2 0° = I0 the intensity of light transmitted by the analyzer is a maximum so this occurs when the transmission axes of the analyzer and the polarizer are parallel.
  • When θ = 90°, It = I0 cos2 90° = 0 so the intensity of light transmitted by the analyzer is a minimum when the transmission axes of the analyzer and polarizer are perpendicular to each other.

Example Question

Unpolarized light with an intensity of Io = 16 W/m2 is incident on a pair of polarisers.

  • The first polariser has its transmission axis aligned at 50o from the vertical.
  • The second polarizer has its transmission axis aligned at 20o from the vertical.

Calculate the intensity of the light going through the pair of filters.

 

  • Let us calculate the intensity of the light when it emerges from the first polarizer.

The light is unpolarized, so I1 = 1/2 Io = 8 W/m2.

  • Now let us calculate the intensity of the light when it emerges from the second polarizer

When it emerges from the first polariser the light is linearly polarized at 50o. The angle between this and the transmission axis of the second polarizer is 50o- 20o= 30o

Therefore:

I2 = I1 cos2 30o = 8 x (0.866)2 = 8 x 0.75 = 6 W/m2