The
Pendulum - the maths...
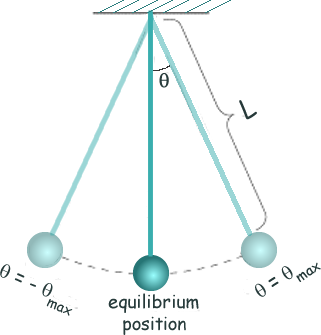
Consider a point pendulum
bob connected to a massless rope or rod that is held at an angle
q from the horizontal.
If you release the mass, then the system
will swing to a position at an angle q from the horizontal on the other side and back again to its starting position. This is one full period of the swing.
It can be determined that:
where
T is the period,
or time for one complete swing,
l is the length
- the distance from the point of suspension to the center of gravity
of the bob. Care has to be taken that the point of suspension is a
point - this can be achieved by clamping the string frimly between
two pieces of card.
g is the acceleration
of gravity.
Forces
acting on the pendulum
When you release
the pendulum bob it will accelerate toward the equilibrium position. As
it passes through the equilibrium position, it will slow down until it
reaches a position - 
, and then accelerate
back. At any given moment, the velocity of the pendulum bob will be perpendicular
to the rope. The pendulum’s path follows an arc of a circle, where
the rope is a radius of the circle and the bob’s velocity is a line
tangent to the circle.
To calculate the forces
acting on the pendulum at any given point in its trajectory it will be
most convenient to choose a y-axis that runs parallel to the rope. The
x-axis then runs parallel to the instantaneous velocity of the bob so
that, at any given moment, the bob is moving along the x-axis.
Two forces act on
the bob:
the force of gravity,
F = mg, pulling the bob straight downward and
the tension of
the rope FT pulling
the bob upward along the y-axis.
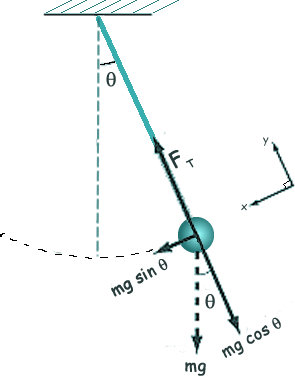
The gravitational
force can be broken down into an x-component of mg sin θ, and a y-component of mg cos θ.
The y
component must balance out the force of tension FT — as the pendulum bob doesn’t
accelerate along the y-axis — so the tension in the rope must also
be mg cos θ.
Therefore,
the tension force is maximum for the equilibrium position and decreases
with θ .
The restoring
force is mg sin θ, so the restoring force is
greatest at the endpoints of the oscillation, and is zero when the pendulum
passes through its equilibrium position.
N.B. The restoring force for the pendulum, mg sin θ, is not directly proportional
to the displacement of the pendulum bob which makes calculating the various
properties of the pendulum very difficult.
Pendula, however, usually only
oscillate at small angles, where sin θ = θ (in radians).
In such cases, we can derive straightforward formulae, which are only
approximations but work well enough in practice.
Click here to consider the energy transitions
About this site
