The human eye, sight defects and their correction

   

You are expected to be able to draw simple diagrams to represent the passage of light through the eye

Make sure that your diagrams clearly show which way the curved surfaces make the light bend! It is good practice to continue the path of a ray through the boundary with a dotted line, draw in a normal to the surface and then draw in the refracted ray The diagrams below do NOT do this - the computer drawn images would have been too cluttered.. but you should practice drawing these diagrams until you can draw them easily and clearly

 

(NB Refraction is only shown at the air/cornea boundary)

You are expected to know:

• What happens to rays of light passing through a normal, short-sighted and long-sighted eye.
• What type of lens is required to correct sight defects.
• How to draw a ray diagram to show the correction
• To understand the problems associated with lens use - see aberration.

Sight Correction Diagrams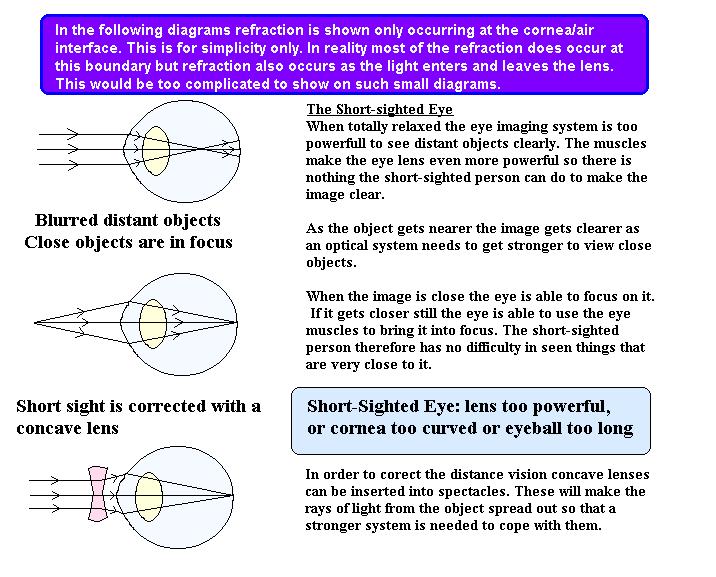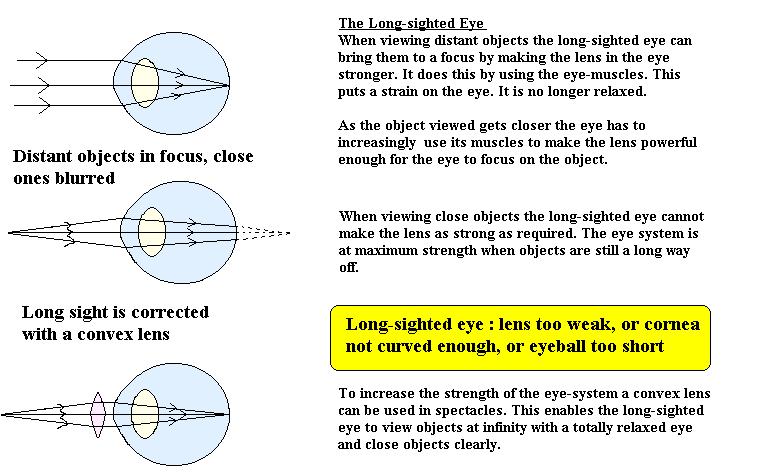

Wearing glasses

When you wear glasses you see the images of the objects not the objects themselves!
The images you see are upright and on the same side of the lens as the objects - therefore the image you see is virtual (its distance has a negative sign). The object distances have a positive sign.
In order to see clearly the image has to be within your range of clear vision (between your near and far points).

Long Sight

A long sighted person cannot see things clearly if they are close to them. Someone with normal sight sees an object when it is only 25 cm from their eye. To a long sighted person that would be blurred. When a person with long sight puts on their spectacles they are able to see objects that are placed at the normal near point.

How does this happen?

Well, the lenses make the image of the object placed at the near point appear to be at the person's actual near point. For example: if a person has an unaided near point of 0.60m they need a convex lens in their glasses to make them able to see clearly an object that is only 25 cm from their eyes. What would be the power of this lens?

The object distance (u) is 25 cm as the object is actually that far from the person's eyes.
The image distance (v) has to be 60 cm as that is the closest distance the person's eyes can focus on.
The image has to be the 'right way up' and 'on the same side of the lens as the object' so it will be virtual.
The lens is convex so the focal length is positive.

So, we have:

u = +0.25 m
v = - 0.60 m

P = 1/f = 1/v + 1/u
= -1/0.60 + 1/0.25
= + 2.3 D

f = 1/P = 0.43 m

Wearing these spectacles will have an effect on the way you view distant objects. It alters the power of the optical system you are using to see with.

The most relaxed your eye can be (flattest lens shape - no use of muscles to squeeze the lens) is when rays that are coming from infinity enter your eye. An object placed at the focal point of a convex lens produces parallel rays so the far point of vision with these glasses on will be the focal length of the lens itself.

Therefore the far point of a person when wearing the lens will be 0.43 m and the range of clear vision will be 25cm to 43 cm.

Short sight

A short sighted person cannot see things clearly if they are far away from them. Someone with normal sight sees an object when it is at infinity. To a short sighted person that would be blurred. When a person with short sight puts on their spectacles they are able to see objects that are placed at the normal far point - infinity.

How does this happen?

Well, the lenses make the image of the object placed at the infinity appear to be at the person's actual far point. For example: if a person has an unaided far point of 0.60m they need a concave lens in their glasses to make them able to see clearly an object that is at infinity. What would be the power of this lens?

The object distance (u) is infinity as the object is actually that far from the person's eyes.
The image distance (v) has to be 60 cm as that is the closest distance the person's eyes can focus on.
The image has to be the 'right way up' and 'on the same side of the lens as the object' so it will be virtual.
The lens is concave so the focal length is negative.

So, we have:

u = infinity and 1/u = 0
v = - 0.60 m

P = 1/f = 1/v + 1/u
= -1/0.60 + 0
= - 1.7 D

f = 1/P = -0.60 m

Wearing these spectacles will have an effect on the way you view close objects. It alters the power of the optical system you are using to see with.

The most stressed your eye can be (fattest lens shape - maximum use of muscles to squeeze the lens) is when rays that are coming from close up to enter your eye.

Let us suppose that the near point of the short sighted person is 20cm. Then the closest an object can be clearly viewed from will be:

f = -0.60 m
v = - 0.20 m

1/f = 1/v + 1/u
-1/0.60 = - 1/0.20 + 1/u
1/u = + 3.33
u = 0.30 m

Therefore the near point of the person when wearing the lens will be 0.30 m and the range of clear vision will be 30 cm to infinity.

The following video is high level biology of the eye - you have been warned!