Topic Menu

Cyber-chess a chess instruction site

Orbital Motion - Kepler's Laws

In the 16th century, a Polish astronomer called Nicolas Copernicus put forward the idea that the Earth and the planets rotate around the Sun as this explained the apparently complex movement of planets in the night sky in a simple way.

Previously, it was held that everything rotated around the Earth and that meant that planets sometimes moved backwards! Copernicus thought the orbits were circles and his ideas caused a lot of controversy.

About 75 years later the German mathematician, Johannes Kepler, made detailed observations and determined that the orbits were not circles, but ellipses. He formulated three empirical laws that descibed how planets and other space objects travel, when in an orbit.

Kepler's first law

Kepler's first law states that the orbit of an object moving around another in space is elliptical with the stationary object located at one of the focal points of the ellipse.

So, the Earth orbits the Sun by following an ellipital path, and the Sun is at a focal point of that ellipse. The same is true for a satellite traveling around the Earth.

It is possible to travel in a circular orbit, but that is a special case - one where the two foci of the ellipse are in the same positions.

An ellipse is an oval geometric shape with two foci (plural of focus).

 

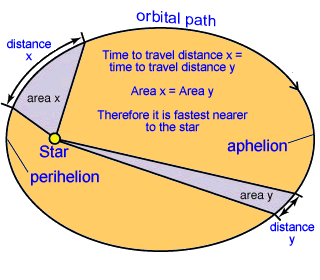
A circle is a special case of an ellipse where both focus points are at the same point—the center of the circle.

Kepler's second law

Kepler's second law states that the orbiting satellite will speed up when it gets closer to the object at the focus. This is caused by the increased effect of gravity on the orbiting object as it gets nearer to what pulling it into the orbital path.

The mathematical statement of the law is that the area swept by the planet or rotating object in in giving time is the same, independent of the distance to the object at the focus.

Areas swept in a given time are equal 

Since the areas are equal, the arc that is further away is shorter, meaning that the speed will be slower. This is true for all orbiting objects.

Kepler's third law

This law shows the relationship for the time required for a planet to move around the Sun and the average distance from the Sun.

The relationship is that the period time squared is proportional to the radius of the path cubed.

T1²/T2² = r1³/r2³

where

T1 is the time is takes the first planet to go around the Sun

r1 is the distance of the first planet from the Sun

T2 is the time is takes the second planet to go around the Sun

r2 is the distance of the second planet from the Sun