Topic Menu

Cyber-chess a chess instruction site

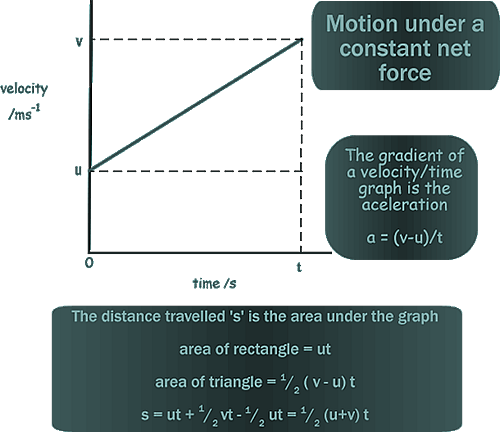
Newton's Equations of Motion

Consider the graphic above. If we plot a graph of an object's motion under the influence of a constant force, we get a graph just like that.

We use letters to represent values:

The initial velocity is u

The final velocity is v

The time of travel is 't'

The distance travelled in that time is 's'

Derivation of the Equations of Motion

We get two relationships that can be expressed as an 'equation of motion' directly from the graph above:

From the gradient we get Equation 1:

v = u + at

From the area under the graph we get Equation 2:

s = ½ (u + v)t

If we replace the v in the second equation with the expression from the first, we can get Equation 3:

s = ½ (u + (u + at))

t = ½ (2u + at))

t = (u + ½ at)t

s = ut + ½at2

If we square the first equation we get Equation 4:

v2 = (u + at)2

v2 = u2 + a2t2+ 2uat

v2 = u2 + 2a (½at2 + ut)

and substitution of (½at2 + ut) as 's' from Equation 3 gives us:

v2 = u2 + 2as

The thing to remember about these equations is they can only be applied to a situation in which a constant net force is acting.There has to be constant acceleration for them to apply.

Most examination questions you will be given to use these equations in will concern objects falling under gravity - air resistance has to be negligible for them to be applicable... and you may be expected to state that air resistance is being ignored.