Topic Menu

Cyber-chess a chess instruction site

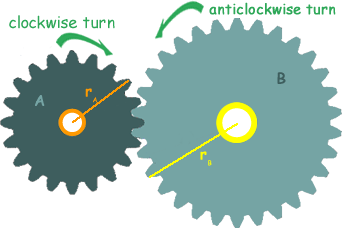
Gears

Gears are wheels with toothed edges that can be made to rotate. They are fixed to an axle or shaft. The teeth of one gear fits into the teeth of another gear. This allows one gear turn the other, meaning one axle or shaft can be used to turn another shaft.

As one gear turns, the other gear must also turn, as the interlocking teeth push it round. Where the gears meet, the teeth must both move in the same direction.

If gear A is turned clockwise it will make gear B turn anticlockwise. The teeth of A on the interconnecting part will be moving downwards - so they will push the teeth on cog B down too.

 

This means that the gears rotate in opposite directions.

The forces acting on the teeth are identical for both gears, but their moments are different, because the distances from the turning points are different.

FB = FA

rB > rA

so the moment of gear B will be greater than that of gear A

MB > MA

If the driven gear is larger than the driver gear it will rotate more slowly - but with a greater moment. For example, a low gear ratio on a bike or car.

If the driven gear is smaller than the driver gear it will rotate more quickly - but with a smaller moment. For example, a high gear ratio on a bike or car.

Example question

A gear with a radius of 0.1 m is turned by a gear with a radius of 0.05 m.

The moment of the smaller gear is 20 Nm.

Calculate the moment of the larger gear.

For the small gear

M = Fd

20 = F x 0.05

so, F = 20/0.05 = 400 N

Now this is the force on the second gear

So,

M = Fd

M = 400 x 0.1

M = 40 Nm

You can see from this example that turning a gear that has double the radius doubles the turning effect - it is a 2× force multiplier.