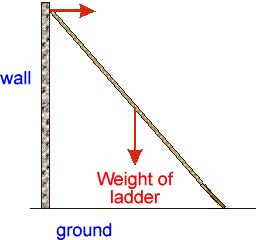
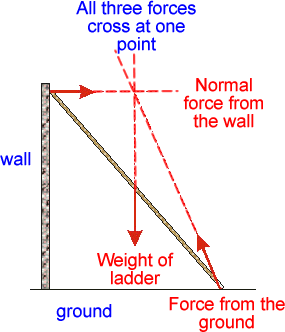
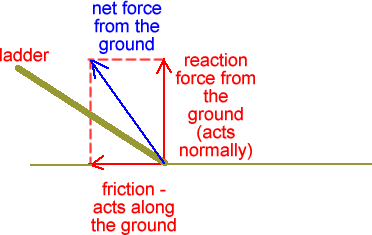
Equilibrium - statics questions Conditions for the Equilibrium of Three Non-Parallel Forces If we say that an object is under the influence of forces which are in equilibrium, we mean that the object is not accelerating - there is no net force acting.The object may still be travelling - but at a constant velocity - but in most questions the object will be stationary. The following pointers will help you to solve problems that involve a body acted on by three co-planar forces.
Example questions
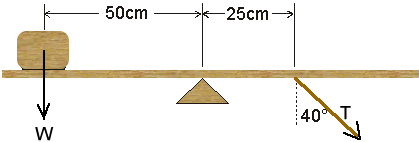
Q2. The diagram below represents a uniform beam which is in equilibrium. The block resting on the beam has a mass of 2.00 kg. A rope is holding the system in equilibrium. Calculate the magnitude of the tension T in the rope. . W = 2.00 × 9·81 = 19.6 N Resolving the tension to give the verical force we get T cos 40o That is then the force making the clockwise moment. So by the principle of moments we get:
(T cos 40o) × 25 = 19.6 × 50 T = 51·2 N
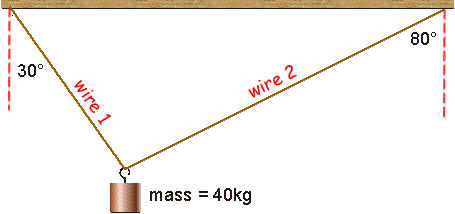
Q3. The object in the diagram below has a mass of 40kg. Calculate the magnitude of the tensions (T1 and T2) in the supporting wires.
The forces acting on the mass are in equilibrium horizontally. Therefore, considering magnitudes only, we can write T1cos 60o = T2cos 10o The forces acting on the mass are also in equilibrium vertically. Therefore, considering magnitudes only, we can write T1cos 30o + T2cos 80o = mg These two equations can be solved simultaneously to find T1 and T2. See free body diagrams for how to simplify questions you have to tackle. |
Follow me...
|