About this site
 |
Elastic Potential Energy
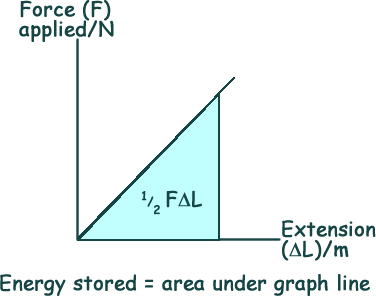
Elastic Potential Energy (sometimes called 'stretch or compressed' potential energy) is found in springs, elastic balls and bands and any 'stretchy' materials. It comes from the structure of the materials and their desire to retain a particular shape. It can be used as a store for energy (hence the word 'potential'). The energy stored is the area under a force/extension graph line.
The spring constant 'k' is the gradient of the Force/extension graph. k = F/ΔL so F = kΔL Area undergraph = ½FΔL = ½ k ΔL2 energy stored in a stretched spring (J) = ½ × spring constant (N/m) × (extension (m))2 Elastic Behaviour
Elastic bands are a good example of this - although most materials exhibit elastic behaviour to some extent. Plastic Behaviour
Atoms that make up a material are arranged in a particular way - when you compress or stretch a material with enough force to alter this arrangement you make the object experience plastic behaviour. You permanently deform the material. Hooke's Law
This means that if you hang weights onto the end of a spring and measure how much the spring stretches for each weight you can plot a graph of your results and show that they are proportional to each other at first and them the proportionality stops. Plot the extension on the x-axis against the weight applied to the spring on the y-axis. You will get a straight line for the initial readings and a curve for the higher ones - if you carry on and add very heavy weights you will cause the spring to deform (it won't conract when you remove the weights) or even break! (fracture).
|
Follow me...
|
To stretch or compress something you need to apply two opposing forces - if you just apply one force you will simply make the object move.
See 
Cyberphysics - a web-based teaching aid - for students of physics, their teachers and parents....
