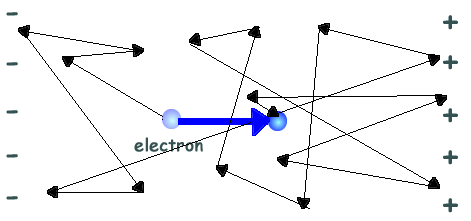
Current (at A Level) : I = nAqv At A Level we start to 'refine' our GCSE understanding of charge movement. The old idea of free electrons whizzing around a circuit has to go! In a piece of metal conductor, at any temperature above absolute zero, loosely held electrons (those in energy states furthest from the nucleus) move randomly, interacting with each other, rapidly changing direction and accelerating and decelerating as they move with what it termed a 'thermal velocity'. Those electrons that are loosely held by the nucleus are called 'free electrons'. You get as many free electrons moving on one direction as in the opposite direction so the net movement of chanrge is zero. But a lot of movement of electrons is going on!
When a potential difference is applied across a conductor, the 'free electrons' gain velocity in the direction opposite to the electric field between successive collisions (and slow down when traveling in the direction of the field). So an electron acquires an overall velocity component in the opposite direction of the electric field when a potential difference is applied. It is still moving 'all higglety pigglety' but with an over all net direction for the velocity.
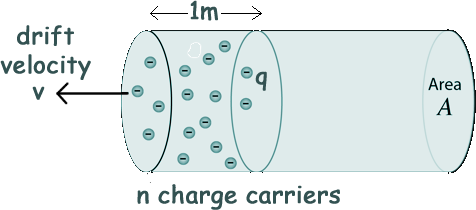
A single electron, if observed would not be seen whizzing in one direction because of the applied field. It would sometimes move in opposition to the field and would be constantly interacting with neighbouring atom electron shells - its path would be a wild zig-zagging path - but overall it would have a tendency to move in opposition to the applied electric field. As a result of this happening to all of the loosely held electrons in the conductor, there is a definite small drift velocity of the millions of free electrons, superimposed on their random motion. There is a tiny charge on each one (1.6 x 10-19 C) but the movement of charge in a given time gives rise ot a current. Therefore a net flow of charge in unit time from those electrons opposite to the direction of the field gives rise to current flow - and the average velocity vector for the electrons in the conductor is called the drift velocity. Let us say that the charge density is n (that there are n charge carriers in a m3 of conductor), and each charge carrier has a charge of q and their drift velocity is v metres per second.
Let A be the cross sectional area of the conductor. Total charge moving in Am3 of conductor = nq Charge moving 1m in one second = vnq Then I = nAqv
If the charge carrier is the electron then that equation becomes I = Anev
|
Follow me...
|