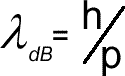Topic Menu

Cyber-chess a chess instruction site

De Broglie wavelength for a particle of matter

 

We can think of waves as particles. They can be thought of as having a mass equivalent and even a momentum - see the photon - now we have to look at matter as waves!

Matter has momentum 'p' - the mass multiplied by the velocity but the photon has momentum expressed in terms of wavelength

pphoton = h/λ

De Broglie (pronounced De Broy) proposed that any particle of matter has a wavelength and wave properties as well as particle properties. Just as a light in a photon has particle properties but is wave also, so an electron or proton (or even YOU) would have a wavelength as well as momentum!

Rearranging the equation (and specifying that the wavelength is associated with matter waves by using a subscript of 'DB' we have:

Note that only moving particles can act like waves! They must have momentum (a non-zero velocity) to have a wavelength.

You will often come across questions in an A level paper that give you the accelerating voltage that a charged particle moves across and nothing else! From this information you have to determine the de Broglie wavelength of the particle.

Let us consider this:

E = QV

Energy gained by a particle of charge Q when moving across a potential difference V will be the product QV.

So the kinetic energy gained by an electron (having a charge 'e') moving across a potential difference of 'V' would be 'eV'

You should know how to do this...

Now let's try a question!

Over what potential difference do you have to accelerate electrons for them to have a wavelength of 1.2 x 10-10 m?

Click here for the answer.

Ready for some more questions?

Click on the icon - questions and answers at A level standard await you!

For more topics that have practice questions associated with them see the upper left menu bar