3.4.1 Further Mechanics Section: |
| Syllabus Extract |
You should be able to: |
Momentum concepts
Force as the rate of change of momentum
F= ∆(mv)/ t∆
Impulse
F∆t =∆(mv)
Significance of area under a force-time graph.
Principle of conservation of linear momentum applied to problems in one dimension.
Elastic and inelastic collisions; explosions.
|
Recall the terms momentum and impulse and their units.
Interpret force v. time graphs - area under the graph is the impulse.
Quote the principle of conservation of linear momentum.
Explain the difference between elastic and inelastic collisions.
 Momentum Structured questions
Momentum Multiple Choice |
Circular motion
Motion in a circular path at constant speed implies there is an acceleration and requires a centripetal force.
Angular speed - ω
ω =v/r= 2πf
Centripetal acceleration - a
a = v2/r = ω2r
Centripetal force
F = mv2/r = mω2r
The derivation of a = v2/r will not be examined.
|
Remember that acceleration is rate of change of velocity - and velocity is a vector - it has direction as well as magnitude of speed associated with it.
With circular motion the object is being constantly pushed towards the circular path's centre.
Circular Motion Multiple Choice
Questions on circular motion link to gravitational fields - motion of planets and satellites.
|
Simple harmonic motion
Characteristic features of simple harmonic motion.
Conditions for shm:
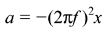
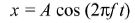
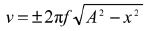
Graphical representations linking x,v,a and t
Velocity as gradient of displacement-time graph.
Maximum speed = 2πfA
Maximum acceleration = (2πf)2A
|
Ensure you can define SHM - they always ask for that - 2 marks!
Get an overall appreciation of displacement from mean position, velocity and acceleration changes.
Graphs are important - can you sketch them?
SHM Structured questions
|
Simple harmonic systems
Study of mass-spring system:
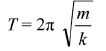
Study of simple pendulum:
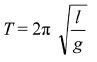
Variation of Ek, Ep and total energy with displacement, and with time. |
Practical techniques must be appreciated - this is an opportunity for the examiner to check your experimental techniques.
SHM Multiple choice |
Forced vibrations and resonance
Qualitative treatment of free and forced vibrations.
Resonance and the effects of damping on the sharpness of resonance.
Phase difference between driver and driven displacements.
Examples of these effects in mechanical systems and stationary wave situations. |
This leads to 'wordy' answers, ensure you understand all of the terms and can define them with precision.
|
About this site
