Errors and Uncertainties at A Level

When most students perform experiments in practical sessions they are worried when they find that they obtain 'errors' in their result. This is because they understand 'error' as being due to some mistake they have made or blunder they have committed.

So, thinking that they are 'wrong' somehow, they are worried they will get low marks or have to 'redo' the experiment to eliminate the 'error'. This leads to some students actually making up results rather than recording what they see. This defeats the object of the practical classes in school, which is to teach you how to use equipment safely and compitently and to understand its limitations.

Error in practical experiments is inevitable, and your understanding of that it important. Errors are not to be confused with mistakes. For example, a badly plotted point on a graph or a transcription error when taking data from one table to another is a mistake NOT an error.

Errors are not a 'mistake' that can be avoided with care (although practice and experience can minimise some random errors). But identifying sources of error and assessing how best to minimise them is an essential part in taking measurements. As long as an experimenter is correct in the performance of the experiment errors are expected (in fact a 'perfect' set of results are highly suspicious!).

It is not the responsibility of the experimenter to eliminate 'the error' but it is their responsibility to understand how different types of error can occur in their measurements and how to reduce all these sorts of error to minimum.

Systematic errors and random errors in measurements.

A systematic error is 'reproducible inaccuracy introduced by faulty equipment, calibration or technique'.

Systematic errors always affects measurements by the same amount or by the same proportion, provided that readings are taken the same way each time.

They are predictable.

Systematic errors are cannot be identified by repeated trials in a single experiment using the same instrument or same method. That is because systematic errors (which includes zero errors) are due to a problem with the instrument or method itself, and therefore do not fluctuate in a repeated trials in a single experiment.

Random error is indefiniteness of result introduced by finite precision of measurement or statistical variations - a measure of fluctuation after repeated experimentation.

Random errors are random in nature because they are due to tiny changes in the behaviour of the experimenter in conducting the experiment or making repeated observations.

It comes from unpredictable changes during an experiment.

The extent of random errors can beidentified through repeated trials in a single experiment.

Random errors cannot be eliminated from an experiment, but most systematic errors can be reduced.

Understand the distinction between precision and accuracy

Accurate measurement: Any observed measurement is an accurate measurement if it is close to the true value. The accuracy of a measurement determines the discrepancy or difference between the observed value and the 'true value'.

The less the discrepancy between the measured value and the true known value, more accurate is the measurement.

Percentage error determines the accuracy of the measurement.

The greater the percentage error, less accurate is the measurement.

Precision determines how close the readings of different trials carried out repeatedly in a single experiment are to each other. If you get virtually the same answer when repeating readings you have precision.

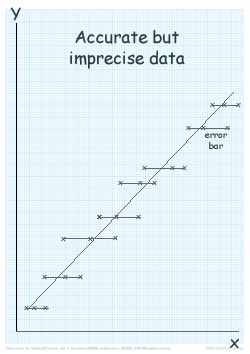
Precision alone is not sufficient for measurement to be accurate.

For example if using a micrometer screw guage to measure the diameter of the spherical ball, we can be pleased to see the readings of repeated trials are close to each other, only to later find that our micrometer screw guage had a zero error that we did not take into account in our initial measurements.

So, though our measurements were precise they were not accurate.

The accuracy of an experiment is a measure of how close the result of the experiment is to the true value; the precision is a measure of how repeatable are the results that have been determined, without reference to agreement with a true value.

Precision is a measure of the reproducibility of the result in a given experiment and how carefully readings have been taken.

Click here to find out about calculating percentage uncertainties.

Click here to read information on writing practical reports that was extracted from a circular sent out by the AQA examining board - back in the days when full practical reports were needed.