About this site
 |
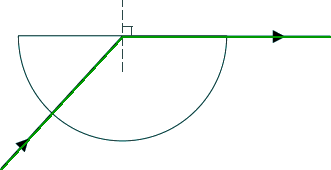
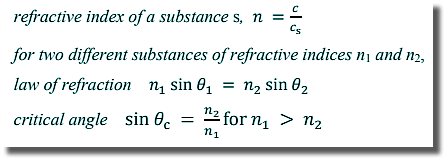Refraction and Total Internal Reflection Q2. The diagram below shows a ray of monochromatic green light incident normally on the curved surface of a semicircular glass block.
(a) The angle of refraction of the ray at the plane surface is 90°. Refractive index of the glass used = 1.6 Calculate the angle of incidence of the ray on the flat surface of the block.
sin θc = 1/1.6 = 0.625 θc = 39 o [1 mark] (b) A thin film of liquid is placed on the flat surface of the glass block as shown in the diagram below.
The angle of incidence is changed so that the angle of refraction of the green light ray at the glass–liquid interface is again 90°. The angle of incidence is now 58°. Calculate the refractive index of the liquid. sin θc = n2/n1 sin 58o = n2/1.6 n2 = sin 58o x 1.6 n2 = 1.4 [2 marks] (c) The source of green light is changed for one that contains only red and blue light. For any material red light has a lower refractive index than green light, and blue light has a higher refractive index than green light. The angle of incidence at the glass–liquid interface remains at 58°. Describe and explain the paths followed by the red and blue rays immediately after the light is incident on the glass–liquid interface. Red light lower refractive index - refracted less than green light (less than 90o angle) Blue light higher refractive index - refracted more than the green light - exceeding critical angle [3 marks] (Total 6 marks) |
Follow me...
|
The angle of incidence produces an angle of refraction of 90o so it is the citical angle.
Cyberphysics - a web-based teaching aid - for students of physics, their teachers and parents....
