Diffraction - Multiple Choice Answers Q1. Monochromatic light of wavelength 590 nm is incident normally on a plane diffraction grating having 4 × 105 lines m−1 . An interference pattern is produced. What is the highest order visible in this interference pattern?
Q2. Light of wavelength λ is incident normally on a diffraction grating of slit separation 4λ. What is the angle between the second order maximum and third order maximum?
Q3. Monochromatic light of wavelength 490 nm falls normally on a diffraction grating that has 6 × 105 lines per metre. Which one of the following is correct?
d = 1/(number of lines per metre) = 1/(6 × 105) = 1.67 x 10-6 sin θ = n x λ/d sin θ1 = 1 x (490 x 10-9)/( 1.67 x 10-6) = 0.293 sin θ2 = 2 x (490 x 10-9)/( 1.67 x 10-6) = 0.587 θ1 = 17o (so A is true) θ2 = 36o (so B is not true) sin θ3 = 3 x (490 x 10-9)/( 1.67 x 10-6) = 0.880 θ3= 62o (so C is not true) n ∝ d d = 1/(number of lines per metre) so, n ∝1/(number of lines per metre) so increasing the number of lines per meter would no produce more orders but less. (so D is not true)
Q4. Light of wavelength λ is incident normally on a diffraction grating for which adjacent lines are a distance 3λ apart. What is the angle between the second order maximum and the straight-through position?
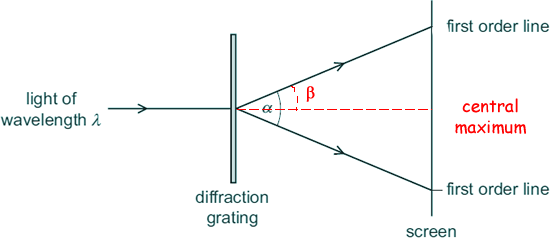
Q5.
Q6. A light source emits light which is a mixture of two wavelength, λ1 and λ2. When the light is incident on a diffraction grating it is found that the fifth order of light of wavelength λ1 occurs at the same angle as the fourth order for light of wavelength λ2. If λ1 is 480 nm what is λ2?
Q7. A diffraction pattern is formed by passing monochromatic light through a single slit. If the width of the single slit is reduced, which of the following is true?
Q8. Light of wavelength λ passes through a diffraction grating with slit spacing d. A series of lines (fringe pattern) is observed on a screen.
Q9. A diffraction grating experiment is set up using yellow light of wavelength 600nm.
The grating has a slit separation of 2.00 μm. What is the angular separation (θ2 – θ1) between the first and second order maxima of the yellow light?
The diffraction grating equation: d sin θ = n λ d sin θ1 = λ sin θ1 = 600 x 10-9 /2.00 x 10-6 = 0.30 θ1 = 17.45° d sin θ2 = 2 λ sin θ2 = 0.60 θ2 = 38.87° θ2 - θ1 = 19.42° - Choice B
Q10. A wave is diffracted as it passes through an opening in a barrier. The amount of diffraction that the wave undergoes depends on both the:
Q11. Which of the following provides evidence that light has a wave nature?
Q12. In a diffraction-grating experiment the maxima are produced on a screen. What causes the separation of the maxima of the diffraction pattern to decrease?
The fringe spacing equation: w = λD/s λ and D increasing will make w increase.... Increasing the distance between the source and grating will have no effect other than reduce the light intensity getting through.... Increasing s will reduce w
Q13. Two waves with amplitudes a and 3a interfere. The ratio of (amplitude at interference maximim)/(amplitude at interference minimum) is:
Amplitude at maximum is the sum of amplitude - 4a Amplitude at the minimum is difference in amplitude - 2a 4a/2a = 2 Q14. White light passes through a single narrow slit and illuminates a screen. What is observed on the screen?
Q15. When light of wavelength 5.0 × 10−7 m is incident normally on a diffraction grating the fourth-order maximum is observed at an angle of 30°. What is the number of lines per mm on the diffraction grating?
d sin θ = nλ
d sin 30o = 4 x 5.0 × 10−7 d = 4 x 5.0 × 10−7/sin 30o d = 4 x 10-6 m number per mm = 10-3/(4 x 10-6) number per mm = 250 (Choice A) Q16. Intensity maxima are produced on a screen when a parallel beam of monochromatic light is incident on a diffraction grating. Light of a longer wavelength can be used or the distance from the diffraction grating to the screen can be increased. Which row gives the change in appearance of the maxima when these changes are made independently?
w = λD/s
Choice B Q17. Light of wavelength 500 nm is passed through a diffraction grating which has 400 lines per mm. What is the angular separation between the two second-order maxima?
d sin θ = nλ n = 2 λ = 500 x 10-9 m
d = 1/(4.0 x 105) m sin θ = nλ/d sin θ = 2 x 500 x 10-9 x 4.0 x 105 sin θ = 0.4 θ = 23.6o
Choice D
|
Follow me...
|