Solutions: Radioactivity Questions
Q6. A radioactive nuclide decays by emitting  particles. The graph shows how the rate of decay At of the source changes with time t
particles. The graph shows how the rate of decay At of the source changes with time t
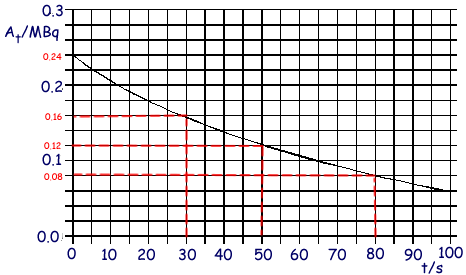
(a) Determine
(i) the half-life of the nuclide,
From the graph - 50 seconds 
(ii) the decay constant,

 = ln 2 / 50 = 0.0139
= ln 2 / 50 = 0.0139 
 = 0.014 s-1
= 0.014 s-1 (unit required!)
(unit required!)
(iii) the initial number of undecayed nuclei present at time t = 0.

At = 0.24 MBq at time t = 0s
N = A/
= 0.24 x 106/0.0139 
= 1.71 x 107
= 1.7 x 107
(5 marks)
(b) Each decay releases 1.0 x 10–12J.
For the time interval between t = 30s and t = 80s, calculate:
(i) the number of nuclei which decay,
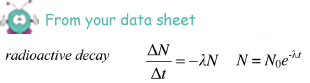
At 30 seconds
N = 1.71 x 107 x e (-0.014 x 30)
N = 1.12 x 107
At 80 seconds
N = 1.71 x 107 x e (-0.014 x 80)
N = 0.56 x 107
during the time interval
1.12 x 107- 0.56 x 107 = 0.56 x 107
(ii) the energy released.
Total energy released = 0.56 x 107 x 1.0 x 10–12J
= 5.6 mJ
(4 marks)
(Total 9 marks)


