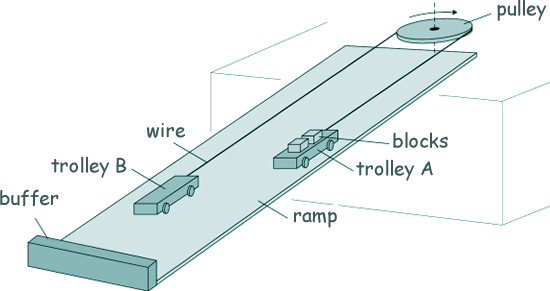
Q7. The diagram below shows a model of a system being designed to move concrete building blocks from an upper to a lower level.

The model consists of two identical trolleys of mass M on a ramp which is at 35° to the horizontal.

The trolleys are connected by a wire that passes around a pulley of negligible mass at the top of the ramp.

Two concrete blocks each of mass 'm' are loaded onto trolley A at the top of the ramp.

The trolley is released and accelerates to the bottom of the ramp where it is stopped by a flexible buffer.

The blocks are unloaded from trolley A, and two blocks are loaded onto trolley B (that is now at the top of the ramp).

The trolleys are released and the process is repeated.

(a) Here is a diagram showing the side view of trolley A when it is moving down the ramp:

The tension in the wire when the trolleys are moving is T.

Draw and label arrows on the side view diagram above to represent the magnitudes and directions of any forces and components of forces that act on trolley A parallel to the ramp as it travels down the ramp.

Both arrows were needed for the mark.

(M+2m) g cos 55^o was okay too, as cos 55^o = sin 35^o.

Arrows not parallel to the ground e.g. weight were ignored as was 'friction'

W was not acceptable for (M +2m)g

[1 mark]

(b) Assuming that no friction acts at the axle of the pulley or at the axles of the trolleys and that air resistance is negligible. Show that the acceleration 'a' of trolley B along the ramp is given by the equation:

Acceleration of both trolleys is of the same magnitude - value 'a'

F = ma

F is the net force acting on the trolley

Trolley B (has no additional masses)

F_B = T - Mg sin 35^o (the tension in the rope is pulling it and the component of its weight is in opposition)

T – Mg sin 35^o = Ma

Trolley A (has two additional masses)

F_A = T - Mg sin 35^o (the component of its weight is pulling it - with the tension in opposition)

(M+2m) g sin 35^o – T = (M+2m) a

Adding the two equations we eliminate T:

(M + 2m) g sin 35^o – Mg sin 35^o = Ma + (M +2m)a

We can then simplify:

Mg sin 35^o + 2mg sin 35^o– Mg sin 35^o = (M + m)2a

a = mg sin 35^o/(M + m) QED

[2 marks]

(c) Compare the momentum of loaded trolley A as it moves downwards with the momentum of loaded trolley B.

Both will move at the same speed as they are attached to each other by the wire - but the velocity of the two will be in opposition as they move in opposite directions.

Momentum = mass x velocity

For A

p_A = (M + 2m)V

For B

p_B = - M V

Momentum of A is greater than that of B and in opposite direction

[2 marks]

(d) In practice, for safety reasons there is a friction brake in the pulley that provides a resistive force to reduce the acceleration to 25% of the maximum possible acceleration.

The distance travelled for each journey down the ramp is 9.0 m.

The following data apply to the arrangement:

Mass of a trolley M = 95 kg

Mass of a concrete block m = 30 kg

Calculate the number of seconds it takes for a loaded trolley to travel down the ramp.

s = 9.0 m

a = ¼ x mg sin 35^o/(M + m) = ¼ x 30 x 9.81 x sin 35^o/125 = 0.338 m/s²

u = 0 m/s

t = ?

s = ut + ½at²

9.0 = ½ x 0.338 x t²

t² = 18/0.338 = 53.25

t = 7.3 s

[3 marks]

(e) It takes 12s to remove the blocks from the lower trolley and reload the upper trolley.

Calculate the number of blocks that can be transferred to the lower level in 30 minutes.

Time to load and travel down ramp = 12 + 7.3 = 19.3 s

30 mins = 30 x 60 s = 1800 s

Number of complete loadings = 1800/19.3 = 93

Two blocks per loading so total number of blocks transported = 186

[2 marks]

(10 Marks Total)