Q1.

A convex lens is placed 0.25 m from an object.

The focused image produced is virtual and is 0.60 m from the lens.

(a) Calculate

(i) the power of the lens,

(ii) the magnification produced.

(3 marks)

(b) Draw a ray diagram to show the formation of the image produced by this lens. The diagram does not have to be to scale, but relevant distances must be marked.

(3 marks)

(c)

(i) What defect of vision is this lens used to correct?

(ii) A person has an unaided near point at 0.60 m and an unaided far point at infinity. Calculate the range of vision of the person when using this lens.

(4 marks)

(Total 10 marks)

Q2.

(a)

(i) Draw a labelled ray diagram to show how a normal eye forms an image of a near point object on the optical axis of the eye. The diagram should show the path of two rays from the object and should indicate clearly the places where refraction occurs.

(ii) Explain why most of the refraction occurs at one of these places.

(4 marks)

(b)

Draw another labelled ray diagram to show where the image of the same object would be formed by an eye suffering from the defect known as hypermetropia or "long-sight". Indicate on your diagram how a suitable correcting lens could be used to bring the image in focus on the retina.

(4 marks)

(c)

A person suffering from hypermetropia has a near point at a distance of 1.25 m from her eyes.

(i) Calculate the power of the correcting lens needed to bring her near point to 0.25 m from her eyes.

(ii) State whether this power is positive or negative.

(3 marks)

(Total 11 marks)

Q3.

A person has a myopic eye with a range of clear vision at distances from his eye of 0.15 m to 0.80m.

(i) Calculate the power of the correcting lens which would allow this eye to produce focused images of distant objects.

(ii) Calculate the new near point position for the eye when using the correcting lens.

(Total 4 marks)

Q4.

A lens is used as shown in the diagram to enable a person with an eye defect to see distant objects clearly.

(i) Name the defect corrected by this lens.

(ii) Determine the power of the lens.

(iii) Draw a ray diagram to show the path through the eye of rays from a distant object when a correcting lens is not being used.

(iv) Draw a ray diagram to show the path through the eye of rays from an object positioned at the uncorrected far-point.

(Total 5 marks)

Q5.

A defective eye has an unaided far point of 2.5 m and an unaided near point of 0.20 m. A correcting lens is used to produce an aided far point at infinity.

(a)

(i) Name the defect of vision affecting the eye.

(ii) State one possible cause of this defect of vision.

(2 marks)

(b) Complete the three ray diagrams below for the defective eye.

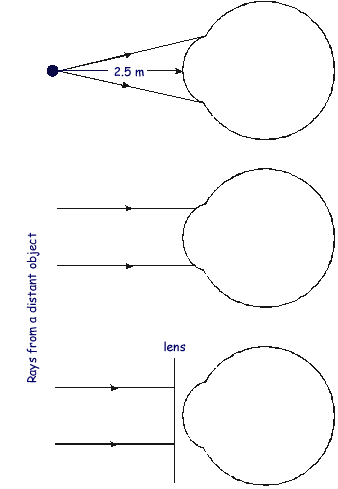
(5 marks)

(c)

(i) Calculate the power of the correcting lens.

(ii) Calculate the aided near point when wearing the correcting lens.

(4 marks)

(Total 11 marks)

Q6.

An eye test shows that a person suffers from astigmatism.

(i) Give the main cause of astigmatism.

(ii) State the effect of astigmatism on the image seen.

(iii) State the type of lens needed to correct this defect of vision.

(iv) Give two quantities which must be known in order to manufacture the correcting lens.

(Total 5 marks)

Q7.

(a) Sketch the response curves for the colour cones of the eye. Label the wavelength axis with a scale appropriate for your curves.

(4 marks)

(b) In terms of receptors,

(i) give the condition for two different images to be resolved by the eye,

(ii) explain why finer detail can be seen in bright light than in dim light.

(3 marks)

(c)

(i) State what is meant by persistence of vision.

(ii) Give an example of a practical situation where persistence of vision is used to advantage.

(2 marks)

(Total 9 marks)

Q8.

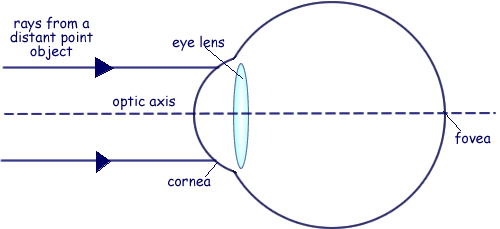
(a) The diagram represents a simplified version of a normal eye, with no sight defects, looking at a distant point object. Complete the paths of the two rays.

(2 marks)

(b) Describe the distribution of receptors over the retina.

(2 marks)

(c)

(i) State the purpose of the iris.

(ii) Describe how this purpose is achieved when the eye is exposed to bright light.

(2 marks)

(d)

(i) State what is meant by accommodation.

(ii) Describe how accommodation is achieved.

(2 marks)

(Total 8 marks)

Q9.

A defective eye has an unaided near point at 0.65 m and an unaided far point at infinity. Calculate

(i) the power of the correcting lens needed to allow the eye to see clearly an object 0.25 m from the eye,

(ii) the furthest distance from the eye that an object can be seen clearly when the correcting lens is used.

(Total 3 marks)

Q10.

(a) The diverging lens in the figure below forms an image of the object.

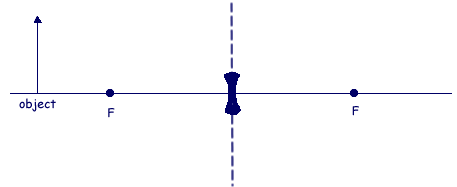
Complete the figure by drawing a ray diagram to show the formation of the image. Label the image.

(2 marks)

(b) A diverging spectacle lens of power –3.0 D is used to correct a defect of vision. When used to view a real object, the image is formed 0.21 m from the lens.

(i) State the defect of vision.

(ii) Calculate the distance of the object from the lens.

(3 marks)

(Total 5 marks)

Q11.

(a) A detailed, coloured object is illuminated by white light. Compare what is seen under high intensity light with that seen under low intensity light by an observer with normal eyesight.

(3 marks)

(b) A person suffering from a vision defect has an unaided far point of 2.0 m.

(i) Name this defect of vision.

(ii) Calculate the power of the correcting lens needed to allow the person to see distant objects clearly.

(iii) The person has an unaided near point at 0.22 m. Calculate the aided near point of the person when using the correcting lens.

(4 marks)

(Total 7 marks)

Q12. A person suffering from long sight has an unaided near point 63 cm from the eye.

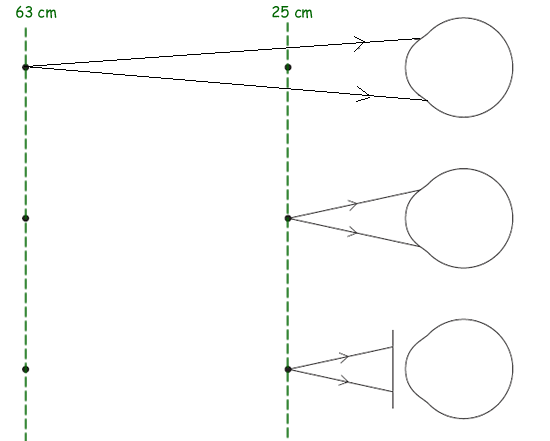
Above are three diagrams (not drawn to scale).

The first two diagrams show rays incident on the unaided eye.

The third diagram shows rays incident on the correcting lens which will allow the person to have an aided near point 25 cm from the eye.

(a) Complete the diagrams to show the passage of the rays to the retina. You may assume that for the eye there is only a single refraction at the cornea of the eye.

(2 marks)

(b) Calculate the focal length of the correcting lens in metres, stating the answer to the appropriate number of significant figures.

(3 marks)

(c) Explain what is meant by persistence of vision and state a practical situation where it is important.

(2 marks)

(Total 7 marks)

Q13.

(a) State the changes which occur in a normal eye when

(i) the eye changes from focussing on a distant object to focussing on a near object, both objects being viewed in bright light

(2 marks)

(ii) the eye changes from viewing an object in very dim light to viewing the same object in bright light.

(2 marks)

(b) State two differences in the perceived image of a coloured object viewed in bright white light compared to the perceived image of the same object viewed in very dim white light.

(2 marks)

(c)

(i) A patient's eye is astigmatic. State the effect of astigmatism on the image produced by the defective eye.

(1 mark)

(ii) State the usual cause of astigmatism.

(1 mark)

(iii) State the shape of lens used to correct astigmatism.

(1 mark)

(Total 9 marks)

Q14.

(a) Rays of light from a point source, 25 cm from a normal eye, enter the eye and are focused forming an image on the retina. State where most refraction occurs and explain why.

(2 marks)

(b) Explain two changes which occur when the eye responds to a wide change in intensity of illumination from very dim light to bright light.

(3 marks)

(c) Explain the term accommodation when applied to the eye.

(2 marks)

(d) A person suffering from long sight is just able to see clearly an object placed 25 cm from the eye when a correcting lens of power +2.4 D is used. Calculate the least distance from the eye to an object that the eye could just see clearly without the use of the correcting lens.

(2 marks)

(Total 9 marks)