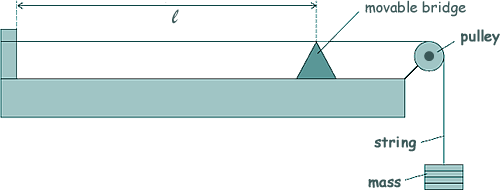
Materials Q5. The diagram shows an arrangement used by Kayjay to investigate vibrations in a stretched nylon string of fixed length l. She measures how the frequency f of first-harmonic vibrations for the string varies with the mass m suspended from it.
The table shows the results of her experiment:
(a) Show that the data in her table are consistent with the relationship f ∝ √T where T is the tension in the nylon string. Tension is proportional to mass. so, f ∝ √m so f2 ∝ m and m/f2 = constant
pretty much constant! QED [2 marks] (b) The nylon string used has a density of 1150 kg m–3 and a uniform diameter of 5.0 × 10–4 m. Determine the length l of the string used. First mark μ = ρA = ρπr2= (ρπd2)/4 μ = 1150 × π (5.0 × 10-4)2/4 μ = 2.258 × 10-4 kg m-1 The use of any pair of m and f substituted into
l = 0.67 m [3 marks] (c) The student uses the relationship in part (a) to predict frequencies for tensions that are much larger than those used in the original experiment. Explain how the actual frequencies produced would be different from those that the student predicts. The diameter reduces when the string is stretched. [2 marks] (Total 7 marks) |
Follow me...
|


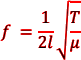 got you the second mark
got you the second mark 


