Topic Menu

Cyber-chess a chess instruction site

Materials

Q3. This question is about the determination of the Young modulus of the metal of a wire.

In an experiment, two vertical wires P and Q are suspended from a fixed support.

The fixed part of a vernier scale is attached to P and the moving part of the scale is attached to Q.

The divisions on the fixed part of the scale are in mm.

An empty mass hanger is attached to Q and the scale is set to zero.

A load is added to the mass hanger so that the extension of Q can be measured as shown in the diagram below.

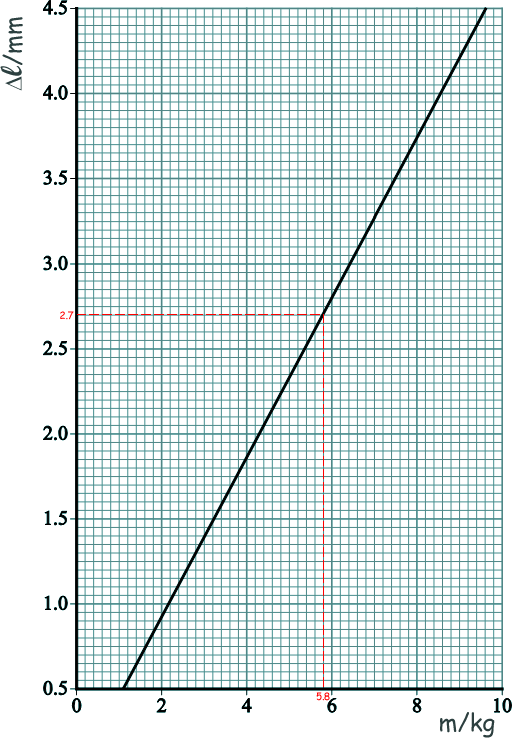
(a) The reading on the vernier scale can be used to determine ∆l, the extension of Q. Determine ∆l using the diagram.

2.7 mm

[1 mark]

(b) The graph below shows how ∆l varies with m, the mass added to the hanger.

Determine the mass added to the hanger shown in diagram above.

5.8 kg

[1 mark]

(c) Lexy uses digital vernier callipers to measure the diameter of Q.

She places Q between the jaws of the callipers and records the reading indicated.

Without pressing the zero button she removes Q and closes the jaws.

Views of the callipers before and after she closes the jaws are shown below:

Calculate the true diameter of Q.

0.44 + 0.07 = 0.51 mm

[1 mark]

(d) The original length of Q was 1.82 m.

Determine the Young modulus of the metal in Q.

∆l = 2.7 mm = 2.7 x 10-3 m

L = 1.82 m

d = 0.51 mm = 0.51 x 10-3 m

A = πr2 = πd2/4 = π (0.51 x 10-3)2/4 = 2.04 x 10-7m2

F = ma = 5.8 x 9.81 = 56.9 N

E = 56.9 x 1.82/(2.04 x 10-7 x 2.7 x 10-3)

E = 1.88 x 1011 N m-2

[4 marks]

(e) Lexy repeats her experiment using a wire of the same original length and metal but with a smaller diameter.

Discuss two ways this change might affect the percentage uncertainty in her result for the Young modulus.

Using a wire of a smaller diameter would produce larger extensions. This would reduce the percentage uncertainty in the extension measurement and therefore in the result for Young Modulus.

But the smaller diameter would increase the percentage uncertainty in measuring the diameter of the wire - and therefore the cross sectional area - resulting in increased uncertainty for the Young Modulus.

[4 marks]

(Total 11 marks)