Q5.

(a) Explain what is meant by the gravitational potential at a point in a gravitational field.

The gravitational potential at a point in a gravitational field is the work done against the field (or energy change) per unit mass when an object is moved from infinity to the point

(2 marks)

(b) Use the following data to calculate the gravitational potential at the surface of the Moon.

mass of Earth = 81 × mass of Moon

radius of Earth = 3.7 × radius of Moon

gravitational potential at surface of the Earth = –63 MJ kg^–1

 

V_E = - GM_E/R_E and V_M = - GM_M/R_M

V_M = - G(M_E x 3.7)/(81 x R_E)

V_M = - G(M_E/ R_E) x 3.7/81 = 3.7/8.1 V_E

=4.7 x 10^-2 x (- 63) = - 2.88 MJ kg^-1

(3 marks)

(c) Sketch a graph on the axes below to indicate how the gravitational potential varies with distance along a line outwards from the surface of the Earth to the surface of the Moon.

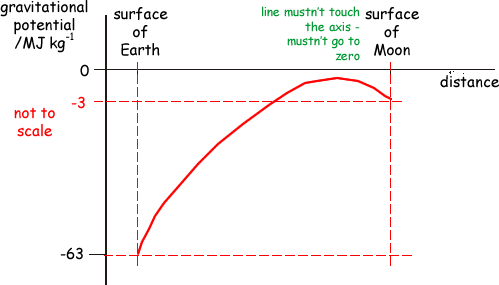
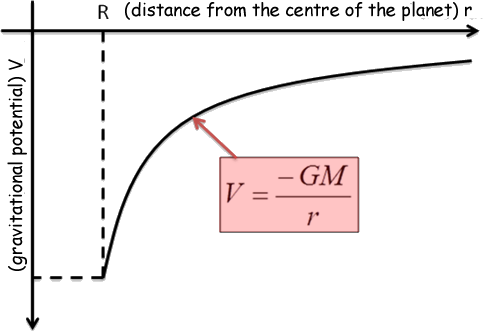
(3 marks)

Curve should start at 'surface of Earth', -63 and finish on 'surface of Moon','–whatever answer to part (b)'

general shape of curving line

peak at a value close to but below zero that is nearer to the Moon than the Earth (3 max)

The GP at a point measures the amount of energy required to bring an object og mass 1kg from infinity, where the value is zero, to that point. As gravity is an attractive force, you have have to do work to move away from another object. This means that you have to give it energy to get its value to zero at infinity. Therefore the values near the Earth or Moon must be negative - you have to add energy to get the value to zero.

The shape of the graph for a single planet is given below - inverse relationship with r in a negative quadrant:

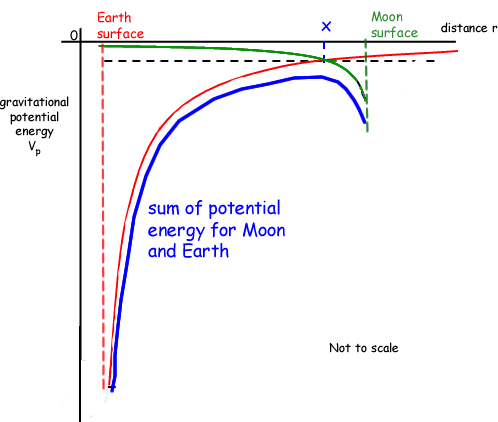
The nearer you are to the mass, and the larger the mass, the more negative the value will be, as you will have to provide more energy to drag the object out to infinity, away from the pull of the planet if it is more massive. The most negative value will occur at the distance that is the radius of the planet you are dealing with.The Earth is a larger mass than the Moon so the values are more negative for the Earth than Moon.

The graph you are asked to plot is what you get when you combine (add) the separate gravitational potential curves that represents the pull of the Earth and the one for the pull of the Moon. In the graph you have to sketch, the (negative) value of the combined curve at any point measures the amount of energy you would need to get away from that place in space to infinity where you would be free of the influence of both masses. Each point will therefore be the sum of the two curves.

The peak of your graph will be at the place, somewhere between the two, where you require the least amount of energy to escape the Earth-Moon system. It will be at the point where the gravitational field strength from the two heavenly bodies is equal and opposite, thus cancelling out the gravitational pull of the two - g is given by 'potential gradient', and at this point the gradient of the gravitational potential graph is zero. So g_moon = -g_Earth

The potential gravitational energy doesn't cancel out at this zero force point as you will always need energy to escape to infinity from the joint force of attraction from the two masses. That amount of energy is the difference between the top of the curve and the axis. therefore if you make the line go to zero you will miss out on a mark!

 

(Total 8 marks)