Gravitational Fields Questions
Q2.
(a)
(i) State the relationship between the gravitational potential energy, Ep, and the gravitational potential, V, for a body of mass m placed in a gravitational field.

The relationship between them is that Ep equals the product of the mass m and the gravitational potential V
or Graviational potential is gravitational potential energy per unit mass (or per kg)
(1 mark)
(ii) What is the effect, if any, on the values of Ep and V if the mass m is doubled?
The value of Ep is doubled 
but the value of V is unchanged 
(2 marks)
(b)
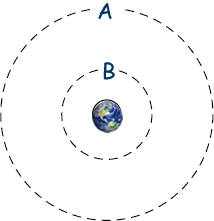
The diagram above shows two of the orbits, A and B, that could be occupied by a satellite in circular orbit around the Earth, E.
The gravitational potential due to the Earth of each of these orbits is:
| orbit A |
– 12.0 MJ kg–1 |
| orbit B |
– 36.0 MJ kg–1 |
(i) Calculate the radius, from the centre of the Earth, of orbit A.
V = -GM/r so r = -GM/V

rA = - (6.67 x 10-11 x 5.98 x 1024)/(-12.0 x 106)  = 3.32 x 107
= 3.32 x 107
rA = 3.3 x 107 m 
(2 marks)
(ii) Show that the radius of orbit B is approximately 1.1 × 104 km.
rAVA = rBVB
rB = rA x VA/VB
VA/VB = 1/3
rB = 3.32 x 107/3  = 1.11
= 1.11
rB = 1.1 x 107m QED
(1 mark)
(iii) Calculate the centripetal acceleration of a satellite in orbit B.
g = GM/rB2
g = (6.67 x 10-11 x 5.98 x 1024)/(1.11 x 107)2
g = 3.2 ms-2
(2 marks)
(iv) Show that the gravitational potential energy of a 330 kg satellite decreases by about 8 GJ when it moves from orbit A to orbit B.
ΔEp = mΔV
ΔEp = 330 × (–12.0 –(–36.0)) × 106
ΔEp = 330 × 24.0 × 106
ΔEp = 7.9 × 109 J ≈ 8 GJ QED 
(1 mark)
(c) Explain why it is not possible to use the equation 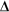 Ep = mg
Ep = mg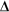 h when determining the change in the gravitational potential energy of a satellite as it moves between these orbits.
h when determining the change in the gravitational potential energy of a satellite as it moves between these orbits.
It is not possible to use the equation because g is not constant over the distance involved. 
Or because g decreases as height increases 
Or because work done per metre decreases as height increases 
Or field is radial and/or not uniform 
(1 mark)
(10 marks Total)


