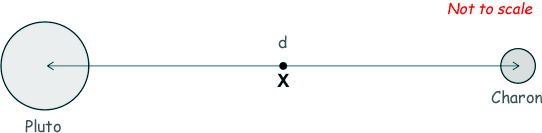Topic Menu

Cyber-chess a chess instruction site

Gravitational fields - Multiple Choice

Q21. Which one of the following statements about Newton's law of gravitation is correct?

Newton's law of gravitation explains:

A the origin of gravitational forces.
B why a falling satellite burns up when it enters the Earth's atmosphere.
C why projectiles maintain a uniform horizontal speed.
D how various factors affect the gravitational force between two particles.

 

Q22. If an electron and proton are separated by a distance of 5 × 10–11m, what is the approximate gravitational force of attraction between them?

A
 2 × 10–57 N
B
 3 × 10–47 N
C
 4 × 10–47 N
D
 5 × 10–37 N

F = 6.67 x 10-11 x 9.11 x 10 -31 x 1.67 x 10 -27 /(5 × 10–11)2 = 4.06 x 10-47 N

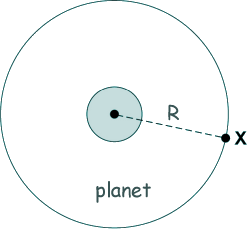
Q23.A spherical planet of uniform density ρ has radius R. Which line, A to D, in the table gives correct expressions for the mass of the planet and the gravitational field strength at its surface?
Mass of the planet
Gravitational field strength at the surface
A
B
C
D

 

There is no need for equation manipulation here - it is a matter of reasoning....

The mass of the planet will depend on the cube of the radius - B or D

Gravitational field strength at the surface will depend on R so A or B

Therefore it must be choice B!

 

Q24. Charon is a moon of Pluto that has a mass equal to that of Pluto.

The distance between the centre of Pluto and the centre of Charon is d.

X is the point at which the resultant gravitational field due to Pluto and Charon is zero.

What is the distance of X from the centre of Pluto?

A
2/9 d
B
2/3 d
C
3/4 d
D
8/9 d

 

g = GM/r2

At X:

Pluto's gravitational field = Charon's gravitational field

GM/X2 = GM/9(d-X)2

Cancel G and M:

X2 = 9(d - X)2

Taking the root of each side, we get:

X = 3(d - X)

X = 3d - 3X

So 4X = 3d

X = ¾d

Choice C

 

Q25. The distance between the Sun and Mars varies from 2.1 × 1011 m to 2.5 × 1011 m. When Mars is

closest to the Sun, the force of gravitational attraction between them is F.

What is the force of gravitational attraction between them when they are furthest apart?

 

 

A
0.71F
B
0.84F
C
1.2F
D
1.4F

 

F ∝1/r2

F1r12 = F2r22

F(2.1 × 1011)2 = F2(2.5 × 1011)2

F2 = F x (2.1 × 1011)2/(2.5 × 1011)2

F2 = F x 2.12/2.52

F2 = 0.71F

Choice A

 

Q26. A satellite X of mass m is in a concentric circular orbit of radius R about a planet of mass M.

What is the kinetic energy of X?

A
GMm/2R
B
GMm/R
C
2GMm/R
D
4GMm/R

In a circular orbit:

F = mv2/r

So for the satellite:

v = √(FR/m)

The force holding it in orbit is gravitational, so:

F = GMm/R2

∴ the velocity of the satellite is given by v = √[(GmM/R2) x (R/m)]

v = √(GM/R)

Now, the kinetic energy of the satellite is given by EK = ½mv2, so:

EK = ½m(GM/R)

EK = GMm/2R

Choice A