Q11. When at the surface of the Earth, a satellite has weight W and gravitational potential energy U.

It is projected into a circular orbit whose radius is equal to twice the radius of the Earth.

Which line, A to D, in the table shows correctly what happens to the weight of the satellite and to its gravitational potential energy?

 

Weight is due to the gravtiational pull of the planet:

W = mg

Now, g = GM/r² so Wr² = constant

W₁r₁² = W₂r₂²

W₁ = W

r₁ = r

r₂ = 2r

∴ Wr² = W₂ x 4r²

W₂ = ^W/₄

Gravitational potential energy is the product of mass and gravitational potential V.

V = - GM/r

and let us make the mass be 'm'

At the surface:

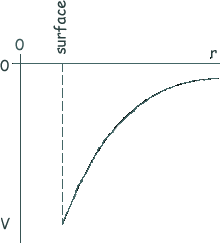
U = - mGM/r

At height r above the surface it would be - mGM/2r = ½U

In other words it would have halved.

So it changed by ½U

Choice B

Q12. The sketch graph shows how the gravitational potential, V, varies with the distance, r , from the centre of the Earth.

What does the gradient of the graph at any point represent?

 

V = - GM/r

so Vr = a negative constant

and the graph of an inverse relationship is shown in the negative quadrant.

You are asked about the gradient.

The gradient of the graph is ΔV/Δr and you are given that relationship on your data sheet.

ΔV/Δr = - g

Choice A

 

Q13. Near the surface of a planet the gravitational field strength is uniform and for two points, 10 m apart vertically, the gravitational potential difference is 3 J kg^–1.

How much work must be done in raising a mass of 4 kg vertically through 5 m?

Points 5 metres apart will have gravitational potential difference of 1.5 J kg^–1.

4 kg are lifted so 6J work is done.

 

Q14. What would the period of rotation of the Earth need to be if objects at the equator were to appear weightless?

The centripetal force is equal to the weight of the object if the object is just able to spin without acceleraing towards the Earth.

If the weight is greater than the centripetal force it will 'fall under gravity'.

If it is less than the centripetal force it will orbit out from the planet's pull.

mv²/r =mg

so, v²/r =g

and v = root of rg = root of (6.37 x 10⁶ x 9.81) = =7905

Now, we can find the speed of rotation by looking at distance travelled (circumference of Earth) and time for one revolution - the period T.

v = 2πr/T

Equating these two calculations of speed we get:

T = 2π x 6.37 x 10⁶ /7905

T = 5063 seconds

T = 1.4 hours

Choice B

 

Q15. The Earth has density ρ and radius R.

The gravitational field strength at the surface is g.

What is the gravitational field strength at the surface of a planet of density 2ρ and radius 2R?

 

density = mass/volume

Volume depends on r³

density depends on mass/r³

If the radius doubles then the density will decrease by a factor of 8 (2³).

We are told that the planet's density has doubled - that means that the mass must have increased by a factor of 16.

Graviational field strength depends directly on mass and inversely on radius squared, it therefore increases by a factor of 16 (because of the mass increase) and decreases by a factor of 2² (because of the radius increase)

Overall that will give an increase of a factor of 16/4 = 4

Choice C

 

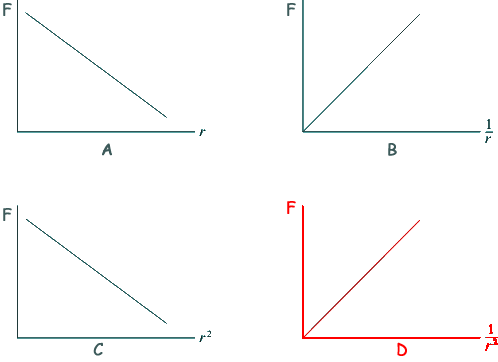
Q16. Which one of the following graphs correctly shows the relationship between the gravitational force, F, between two masses and their separation r?

 

 

The relationship is an inverse squared one - so D is the solution.

 

Q17. Which one of the following could be a unit of gravitational potential?

 

Gravitational potential is 'V'.

On the data sheet you have ΔW (work in joules) = VΔm (mass in kg)

So the unit must be J kg^–1

Q18. The radius of a certain planet is x times the radius of the Earth and its surface gravitational field strength is y times that of the Earth.

Which one of the following gives the ratio ?

 

The gravitational field strength of the planet depends directly on the mass of the planet and inversely on the square of the radius.

Mass = a constant x gr²

An increase of a factor of y will result from an increase of a factor of yx² of mass.

B is the solution

 

Q19. A planet of mass M and radius R rotates so rapidly that loose material at the equator only just remains on the surface.

What is the period of rotation of the planet?

 

speed of rotation = circumference of the Earth/time period of rotation.

So, v = 2πR/T and T = 2πR/v

When loose material only just stays in place it means that the centripetal force is equal to the weight of the object if the object is just able to spin without acceleraing towards the Earth.

If the weight is greater than the centripetal force it will 'fall under gravity'.

If it is less than the centripetal force it will orbit out from the planet's pull.

mv²/R =mg

so, v² =gR

From the equation sheet g = GM/R²

so v² = GM/R

and v = square root of (GM/R)

Therefore T = 2πR / square root of (GM/R)

T = 2πR x square root of (R/GM)

T = 2π x square root of (R³/GM)

Choice D

 

Q20. As a comet orbits the Sun the distance between the comet and the Sun continually changes.

As the comet moves towards the Sun this distance reaches a minimum value.

Which one of the following statements is incorrect as the comet approaches this minimum distance?