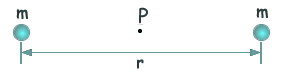Q1 Masses of M and 2M exert a gravitational force F on each other when the distance between their centres is r.

What is the gravitational force between masses of 2M and 4M when the distance between their centres is 4r?

 

F ∝Mm/r²

Increasing the mass product from 2 to 8 would increase F by a factor of 4

Quadrupling the radius would decrease F by 4²

Combining the two factors we get ⁴/₁₆ = ¹/₄ = 0.25

Choice A

 

Q2 A planet has a radius half the Earth's radius and a mass a quarter of the Earth's mass.

What is the approximate gravitational field strength on the surface of the planet?

 

g ∝M/r²

Reducing the mass to a quarter would reduce g by a quarter

Halving the radius would increase g by 2²

Therefore the two factors would cancel each other out, and g would be the same as on Earth.

Choice C

 

Q3. At the surface of the Earth:

the gravitational field strength is g.

the gravitational potential is V.

The radius of the Earth is R.

An object, whose weight on the surface of the Earth is W, is moved to a height 3R above the surface.

Which line, A to D, in the table gives the weight of the object and the gravitational potential at this height?

 

Weight is due to the gravtiational pull of the planet:

W = mg

Now, g = GM/r² so Wr² = constant

W₁r₁² = W₂r₂²

W₁ = W

r₁ = r

r₂ = 4r (r (radius of the planet) + 3R above the surface)

∴ Wr² = W₂ x 16r²

W₂ = ^W/₁₆

Gravitational potential energy is the product of mass and gravitational potential V.

V = - GM/r

and let us make the mass be 'm'

At the surface:

V = - mGM/r

At height 3r above the surface it would be - mGM/4r = ¼V

Choice A

 

Q4. A satellite of mass m travels in a circular orbit of radius r around a planet of mass M.

Which one of the following expressions gives the angular speed of the satellite?

The time taken for one cycle of the path is T (the period)

The length of the path is 2πr (the circumference of a circle)

So

v = 2πr/T

 

The angular velocity ω = Δθ/Δt

To make one full revolution Δθ would be 2π (as there are 2π radians in a full circle)

Period T is the time taken for one full cycle - or one full revolution

So we have Δθ = 2π and Δt = T

So we get:

ω =2π/T

But 2π/T = v/r

so, ω =v/r

In a circular orbit:

F = mv²/r

So for the satellite:

v = √(Fr/m)

The force holding it in orbit is gravitational, so:

F = GMm/R²

∴ the velocity of the satellite is given by v = √[(GmM/r²) x (r/m)]

v = √(GM/r)

Therefore ω = √(GM/r)/r

ω = √(GM/r³)

Choice D

 

Q5. Which one of the following has different units to the other three?

 

Q6. The diagram shows two objects of equal mass m separated by a distance r.

Which line, A to D, in the table gives the correct values of the gravitational field strength and gravitational potential at the mid-point P between the two objects?

Gravitational field strength is a vector. Therefore pulls in opposite direction can canel each other out. At the midpoint the opposing forces will cancel the effect of each other.

Therefore the result will be zero.

Gravitational potential is not a vector. But work either has to be put in or is done by the system when an object is moved from a point therefore it has a sign.

For an object placed at point P work would have to be done against the pull of both masses to move it to infinity - the result is therefore the sum of the potentials and the potential will be the expression not the zero

 

Q7. Mars has a diameter approximately 0.5 that of the Earth, and a mass of 0.1 that of the Earth.

If the gravitational potential at the Earth’s surface is –63 MJ kg^–1, what is the approximate value of the gravitational potential at the surface of Mars?

Vr/M = -G (a constant) so

V_Er_E/M_E = V_Mr_M/M_M

V_M = V_E x M_M/M_E x r_E/r_M

V_M = -63 x 0.1 x 2

V_M = 12.6 MJ kg^–1

Choice A

Q8. A small mass is situated at a point on a line joining two large masses m_l and m₂ such that it experiences no resultant gravitational force.

If its distance from the mass m₁ is r₁ and its distance from the mass m₂ is r₂, what is the value of the ratio ?

 

The force from each large mass on the small mass is equal in magnitude (opposite in direction)

∴ m₁/r₁² = m₂/r₂²

r₂²/r₁² = m₂/m₁

r₁²/r₂² = m₁/m₂

r₁/r₂= (m₁/m₂)^0.5

Choice C

Q9. A projectile moves in a gravitational field. Which one of the following is a correct statement for the gravitational force acting on the projectile?

 

The projectile is a mass - the gravitational field lines show the direction that the gravitational force acts on a mass, so the answer is A.

The initial movement of the projectile is at right angles to the field and its motion will follow a parabolic path... but you are not asked that!

Q10. The diagram shows two positions, X and Y, at different heights on the surface of the Earth.

Which line, A to D, in the table gives correct comparisons at X and Y for gravitational potential and angular velocity?

 

All points on the Earth's surface travel at the same angular velocity - the Earth rotates 360 degrees in a day and all points on it rotate through the same angle on a given time period.

Gravitational potential increases with height - GCSE stuff really!