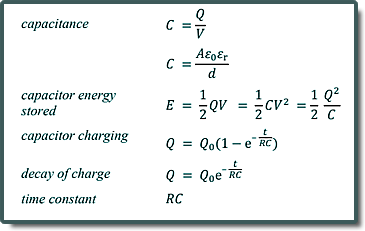Topic Menu

Cyber-chess a chess instruction site

Capacitors - Multiple Choice

Q21. A parallel-plate capacitor is fully charged and then disconnected from the power supply.

A dielectric is then inserted between the plates.

Which row correctly identifies the charge on the plates and the electric field strength between the plates?

 
Charge
Electric field strength
A
Stays the same
Increases
B
Increases
Decreases
C
Increases
Increases
D
Stays the same
Decreases

 

Click here to read up on dielectrics

Choice D

 

Q22. A capacitor of capacitance C has a charge of Q stored on the plates.

The potential difference between the plates is doubled.

What is the change in the energy stored by the capacitor?

C = Q/V

Q is constant - V doubles - so C will halve

E1 = ½CV2

E2 = ½C(2V)2 = ½CV2 x 4 = 2CV2

E2 - E1 = 2CV2 - ½CV2 = 3/2CV2

But V = Q/C so:

E2 - E1 = 3/2C(Q/C)2

E2 - E1 = 3/2 Q2/C

Choice C

Q23. A capacitor consists of two parallel square plates of side l separated by distance d.

The capacitance of the arrangement is C.

What is the capacitance of a capacitor with square plates of side 2l separated by a distance ½d ?

A
C
B
2C
C
4C
D
8C

 

C = Aε0εr/d

A (proportional)increases by a factor of 4 to C increases by a factor of 4

d (inversely proportional) decreases by a factor of 2, to C increases by a factor of 2

Combine factors - 4 x 2 = 8

Choice D

 

Q24. A capacitor of capacitance 120 µF is charged and then discharged through a 20 kΩ resistor.

What fraction of the original charge remains on the capacitor 4.8 s after the discharge begins?

A
0.14
B
0.37
C
0.63
D
0.86

 

The equation we are given on the equation sheet is for a capacitor discharging.

Q repesents the charge discharged by the capacitor in time t:

Q = Q0(1 - e-t/RC)

Q /Q0= 1 - e-t/RC

t/RC = 4.8/(20 x 103 x 120 x 10-6) = 2

Q /Q0= 1 - e-2

Q /Q0 = 0.86

Therefore 86% of the charge has been discharged after that time - this leaves 14% still on the capacitor.

Choice A