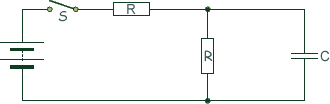
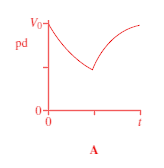
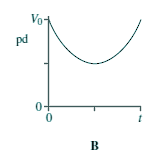
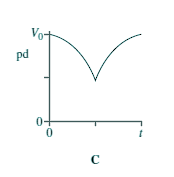
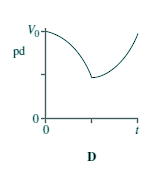
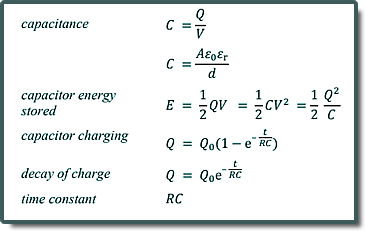Capacitors - Multiple Choice

Q11. When switch S in the circuit is closed, the capacitor C is charged by the battery to a pd V₀.
The switch is then opened until the capacitor pd decreases to 0.5 V₀, at which time S is closed
again. The capacitor then charges back to V₀.

 

 

Which graph best shows how the pd across the capacitor varies with time, t, after S is opened?

 

Q12. A 2.0 mF capacitor, used as the backup for a memory unit, has a potential difference of 5.0V across it when fully charged.

The capacitor is required to supply a constant current of 1.0μA and can be used until the potential difference across it falls by 10%.

How long can the capacitor be used for before it must be recharged?

A	10 s
B	100 s
C	200 s
D	1000 s

 

V = IR

R = V/I

R = 5.0/(1.0 x 10^-6)

R = 5 x 10⁶ Ω

time constant = RC = 5 x 10⁶ x 2.0 x 10^-3 

RC = 1.0 x 10⁴ s

----------------------

V = V₀e^-t/RC

If the voltage falls by 10% it will then be 0.9V₀

0.9 = e^-t/10000

t = -ln 0.9 x 10000 = 1059s

Therefore the answer is.

Choice D

Q13. When a capacitor discharges through a resistor it loses 50% of its charge in 10 s.

What is the time constant of the capacitor-resistor circuit?

 

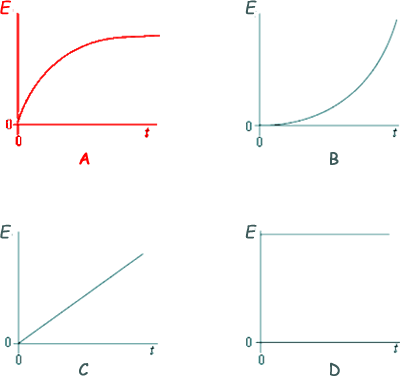
Q14. An uncharged capacitor of fixed capacitance is connected in series with a switch and battery. The switch is closed at time t = 0.

Which graph, A to D, shows how the energy, E, stored by the capacitor, changes with time, t, after the switch is closed?

Energy stored = ½ QV = ½ CV² = ½ Q²/C

The voltage across the capacitor will be the same as graph A - the energy stored will therefore be that graphline value squared - which will be a similar shape - Choice A

Choice D is not possible as energy stored will increase and be zero at time zero.

Choice C is a steady increase with time and we know that voltage increase is rapid at first - so that is not correct..

Choice B is not possible because the voltage increase and therefore the energy stored will level off towards completion of the charge.

 

Q15.The voltage across a capacitor falls from 10 V to 5 V in 48 ms as it discharges through a resistor. What is the time constant of the circuit?

 

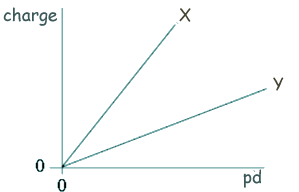
V = V₀e^-t/RC

5 = 10 e^{-0. 48/RC}

ln 0.5 = - 0.048/RC

RC = - 0.048 /ln 0.5

RC = 0.069 s = 69 ms

Choice C

Q16. The graph shows how the charge stored by each of two capacitors, X and Y, increases as the pd across them increases. Which one of the following statements is correct?

 

Q = CV

Therefore as V increases Q will increase

C is constant - the gradient of the graph.

X has a bigger gradient so the capacitance of X is greater than the capacitance of Y.

Choice C

 

Q17. A 1000 μF capacitor and a 10 μF capacitor are charged so that the potential difference across each of them is the same.

The charge stored in the 1000 μF capacitor is Q₁ and the charge stored in the 10 μF capacitor is Q₂.

What is the ratio Q₁/Q₂?

 

Q = CV

V = Q/C

Therefore Q₁/C₁ = Q₂/C₂

Q₁/Q₂= C₁ /C₂ = 1000/10 = 100 - Choice A

Or

You can just reason it -

Capacitor 1 has 100 times the capacitance of capacitor 2

Therefore it will store 100 times more charge as it has a 100x capacity for charge!

 

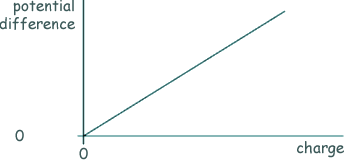
Q18. The graph shows how the potential difference across a capacitor varies with the charge stored by it.

 

Let's consider this graph -

Q = CV

therefore V = Q/C

V = ¹/_C x Q

this corresponds to y = mx

The gradient is therefore ¹/_C

Energy stored is the area under the graph line not the gradient.

Which one of the following statements is correct?

 

Q19. An initially uncharged capacitor of capacitance 10 μF is charged by a constant current of 200 μA. After what time will the potential difference across the capacitor be 2000V?

Q20. A 1000 μF capacitor, X, and a 100 μF capacitor, Y, are charged to the same potential difference.

Which row, A to D, in the table gives correct ratios of charge stored and energy stored by the capacitors?

Charge stored = CV

V is constant so charge stored depends on C

ratio = 1000μ/100μ = 10

-------------------------

Energy stored = ½ QV = ½ CV² = ½ Q²/C

V is constant so energy stored depends on C

ratio will be 1000μ/100μ = 10

 

 

Choice D