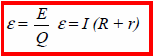Q6.

(a) In the circuit shown in the diagram the battery has an EMF of 6.0 V. With the switch closed and the lamp lit, the reading on the voltmeter is 5.4 V.

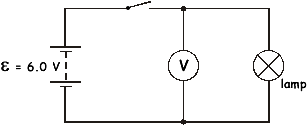
Explain without calculation, why the voltmeter reading is less than the EMF of the battery.

The battery has internal resistance. When a current passes through the circuit work is done (or voltage is used) to drive the current through the battery itself which reduces the value of the open circuit voltmeter reading.

The 'lost volts' correspond to the voltage that drives the current through the battery. You need to explain that this is because the cell has internal resistance and that when a current is driven thorugh the circuit the EMF is shared across the internal resistance and the external resistance of the ciruit. Just saying 'lost volts' will not get you a mark.

 

(3)

(b) A torch is powered by two identical cells each having an EMF of 1.5 V and an internal resistance r. The cells are connected in series. The torch bulb is rated at 1.6 W and the voltage across it is 2.5 V.

(i) Draw the circuit described.

- encapsulate a battery in a dashed box

- show cells and their resistances individually

- above the box indicate the 'net' values (in case that is what the examiner wants) but within the box show individual values.

- incorporate ALL of the info they give you if they ask you to draw a circuit.

- if you add a switch you should put the value on the voltmeter as '3.0V when switch is open and 2.5V when the switch is closed'.

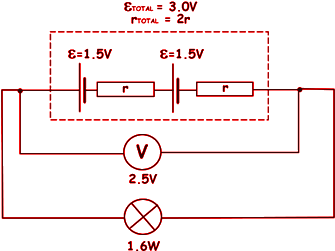
correctly drawn cells in series

resistances in series with the cells and each other.

(ii) Calculate the internal resistance of each cell.

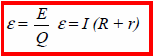
= 3.0 V

V = 2.5 V

(do you see the need for an italic 'V' here?)

(or write V = 2.5 volts)

r = 2r (do you see the need for an italic 'r' here?)

R = ?

I = ?

We have three unknowns, so we need to first find I by some other means…

We can use P = IV (for the lamp) to find the current

P = 1.6W

V = 2.5V

I = P/V

I = 1.6/2.5

I = 0.64 A

We can then eliminate R by replacing IR with V

= I(R + r) = V + Ir

3.0 = 2.5 + 0.64 (2r)

0.5 = 1.28r

r = 0.5/1.28 = 0.39

OR you can do it using 'lost volts'

= I(R + r) = V + Ir

- V = Ir = lost volts = 0.5

0.5 = 1.28r

r = 0.5/1.28 = 0.39

 

(5)

(c) In the circuit below the cell has emf and internal resistance r. The voltage V across the cell is read on the voltmeter which has infinite resistance, and the current I through the variable resistor R is read on the ammeter.

By altering the value of the variable resistor R, a set of values of V and I is obtained. These values, when plotted, give the graph shown below.

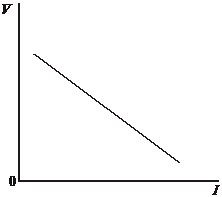
Show how the values of and r may be obtained from this graph. Explain your method.

= I(R + r) = V + Ir

We can rearrange this into the form Y = mx + c which corresponds to the equation of a straight line where 'c' is the intercept and 'm' is the gradient.

V = -rI +

• Y corresponds to V
• x corresponds to I
• m corresponds to -r and
• c corresponds to

The gradient of the line is the (negative) of the internal resistance and the intercept on the Y axis is the EMF of the cell.

(Total 11 marks)