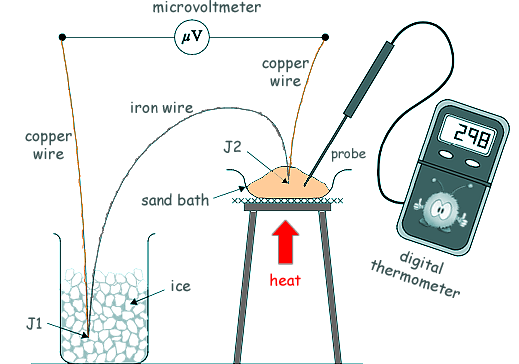
Q12.

Lengths of copper and iron wire are joined together to form junctions J1 and J2.

When J1 and J2 are at different temperatures an emf ε is generated between them.

This emf is measured using a microvoltmeter.

The diagram below shows J1 kept at 0 ºC while J2 is heated in a sand bath to a temperature θ, measured by a digital thermometer.

(a) An experiment is carried out to determine how ε depends on θ.

The results of the experiment are shown in the table below and, below that, a graph is plotted of these data.

 

(i) Plot the points corresponding to θ = 258 °C and θ = 298 °C on the graph.

1 mark for both of the two missing points plotted correctly.

Each had to be plotted to the nearest 1 mm (half a grid square)

The points marked as a neat cross or a circled dot. (Thick points, blobs or uncircled dots got no marks!)

[1 mark]

(ii) Draw a suitable best fit line on the graph.

The examiner expected a continuous smooth best fit line through all 7 points to 1 mm of each point.

No marks for 'dot to dot' straight lines joining the points!

[1 mark]

(iii) Determine the maximum value of ε.

This was awarded for you reading the value from your graph correctly to within a ½ grid square.

I got 1460 μV

[1 mark]

(b) The gradient G of the graph in part (a) is measured for values of θ between 220 °C and 380 °C.

A graph of G against θ is plotted below:

The neutral temperature θ_n is the temperature corresponding to the maximum value of ε.

θ_n can be determined using either of the two graphs.

Explain why a more accurate result for θ_n may be obtained using the second graph.

Finding θ_n from the second graph is easy - you just read off the value where G = 0 (the maximum of the curve has a gradient of zero). Whereas finding it from the curve graph is difficult as the maximum of the curve has a range of values for you to choose from.

[1 mark]

(c) It can be shown that G is given by

G = βθ +α

where α and β are constants

Determine α.

G = βθ + α is the equation of a straight line - the intercept is α.

β is the gradient.

gradient = - 4.0/(364 - 252)
= - 0.0357 μV ^oC ^-2

Choosing the points G = 0 and θ = 280^oC and substituting them into the equation we get:

0 = - 0.0357 x 280 + α

α = 0.0357 x 280

α = 10.0 μV °C ⁻¹

Correctly determining the gradient or uses gradient result with any point on line to determine (vertical) intercept got you a mark.

A result in the range of 9.8 to 10.9 got you the second mark.

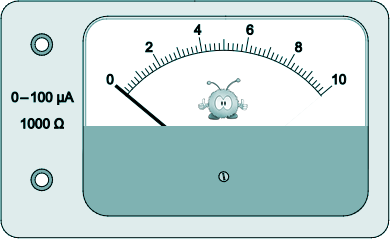
[2 marks]

(d) Enrico decides to carry out a similar experiment. He thinks the meter pictured below could be used as the microvoltmeter to measure ε.

 

When this meter indicates a maximum reading and the needle points to the right-hand end of the scale (full-scale deflection), the current in the meter is 100 µA.

The meter has a resistance of 1000 Ω.

(i) Calculate the full-scale deflection of this meter when used as a microvoltmeter.

Full scale deflection = 100 × 1000 = 100,000 or 10⁵µV

[1 mark]

(ii) The scale on the meter has 50 divisions between zero and full-scale deflection. Discuss why this meter is not suitable for carrying out the experiment.

The resolution (or sensitivity/precision) of the meter is not satisfactory because the largest pd that will be measured is less than 1500 µV and it would be hard to tell different readings apart or only uses 1.5% of the range

 

pd across meter at full-scale deflection ÷ divisions = 10⁵ /50 = 2000 µV per division

[2 marks]

(Total 8 marks)