Questions on EMF and internal resistance
Q11.
In the circuit shown in the diagram, the battery, of negligible internal resistance, has an emf of 30V. The pd across the lamp is 6.0V and its resistance is 12Ω.
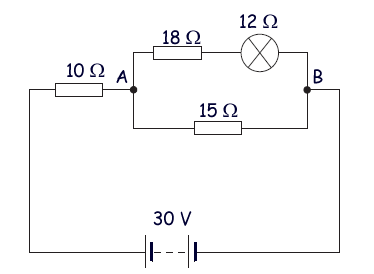
(a) Show that the total resistance of the circuit is 20Ω.
18Ω and 12 ohm resistors are in series .
In series RTOTAL = R1 + R2 = 18 + 12 = 30
They could be replaced by a single 30Ω resistor.
We would then have a 30Ω resistor in parallel with a 15Ω resistor
1/RTotal = 1/R1 + 1/R2 = 1/30 + 1/15 = 3/30
Therefore the parallel arrangement is equivalent to 10Ω. That is in series with a 10Ω resistor
In series RTOTAL = R1 + R2 = 10 + 10 = 20 Ω Q.E.D.
(3 marks)
(b) Calculate
(i) the current supplied by the battery,
V = IR
I = V/R = 30/20 = 1.5 A
(ii) the pd between the points A and B,
Resistance between A and B is 10Ω - half the total resistance. Therefore the voltage across the parallel resistance and the 10 Ω resistor will split equally and the voltage across AB will be 30/2 = 15V
(iii) the current in the lamp.
I = V/R = 6.0/12 = 0.5A
OR
1.5A enters the paralel arrangement. The branch with the lamp in it has double the resistance of the other branch, therefore it wil have half of the current.
0.5 A will go through the branch of the parallel arrangement with the lamp - the other branch will have 1.0A pass through it.
(4 marks)
(c)
(i) What is the power of the lamp, in W?
P = IV = V2/R = 6.02/12 = 36/12 = 3.0W
(ii) What percentage of the power supplied by the battery is dissipated in the lamp?
Power from battery = IV = 30 x 1.5 = 45W
3.0 /45 x 100 = 6.7%
(3 marks)
(Total 10 marks)
About this site
