Q10. A cell of emf, ε, and internal resistance, r, is connected to a variable resistor R. The current through the cell and the terminal pd of the cell are measured as R is decreased. The circuit is shown below.

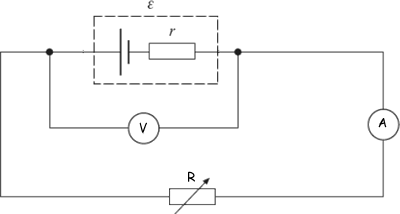
The graph below shows the results from the experiment.

(a) Explain why the terminal pd decreases as the current increases.

The battery has a resistance called the 'internal resistance'. The EMF of the battery is shared across the internal and external resistances. The potential drop across the internal resistance is called the 'lost volts'.

The larger the external resistance in comparison with the internal resistance, the larger the terminal p.d. will be That is because voltage is shared out in proportion to the ratio of resistance.

Current will increase in the circuit if the total resistance is reduced. Therefore as current increases the internal resitance will have a bigger share of the voltage and the external resistance will have a smaller share (because it is smaller!) - resulting in the external potential difference decreasing as current increases.

(2 marks)

(b)

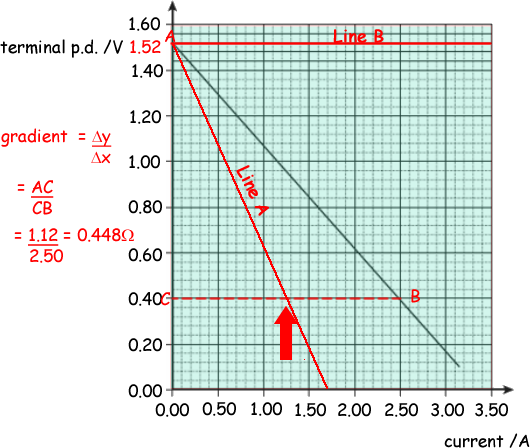
(i) Use the graph to find the emf, ε, of the cell.

ε = I(R - r) but V = IR

ε = V - Ir

V = -Ir + ε

ε is the intercept on the Y-axis.

r is the (negative) gradient

= 1.52 V (± 0.01 V)

(1 mark)

(ii) Use the graph above to find the internal resistance, r, of the cell.

Identifying gradient as r

Clearly showing the working out of the gradient

r = 0.45 ± 0.02 Ω

(3 marks)

(c) Draw a line on the graph above that shows the results obtained from a cell with

(i) the same emf but double the internal resistance of the first cell labelling your graph A.

Same EMF means same intercept

Double the internal resistance means double the gradient. The line must go through y = 1.25, x = 0.40 (± 1.5 squares) for the mark

(2 marks)

(ii) the same emf but negligible internal resistance labelling your graph B.

Same EMF means same intercept - but no internal resitance means the PD will remain at EMF value - a horizontal line!

(1 mark)

(d) In the original circuit shown in part (a), the variable resistor is set at a value such that the current through the cell is 0.89 A.

(i) Calculate the charge flowing through the cell in 15 s, stating an appropriate unit.

I = 0.89 A = 0.89 C/s

therefore in 15s 0.89 x 15 = 13C

(2 marks)

(ii) Calculate the energy dissipated in the internal resistance of the cell per second.

energy dissipated per second = power dissipated (a watt is a joule per second!)

We could use P = IV

In this case 'V' is 'lost volts' but we don't have a value for 'lost volts' at 0.89A and reading it off the graph isn't accurate enough... that is why they gave us a value like that to work from!

Therefore we should use P = I²r instead.

P = 0.89 x 0.45² = 0.36 W

(2 marks)

(Total 13 marks)