Topic Menu

Cyber-chess a chess instruction site

Circular Motion - Multiple choice

Q11. A fairground roundabout makes nine revolutions in one minute.

What is the angular speed of the roundabout?

A
 0.15 rad s–1
B
 0.34 rad s–1
C
 0.94 rad s–1
D
 2.1 rad s–1

 

9 revolutions per minute = 9/60 per second.

1 rev = 2π radians

∴ angular speed = 2π x 9/60 = 0.94 rad s–1

 

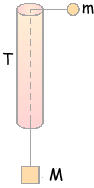
Q12. The figure shows a smooth thin tube T through which passes a string with masses m and M attached to its ends.

Initially the tube is moved so that the mass, m, travels in a horizontal circle of constant radius r, at constant speed, v.

Which one of the following expressions is equal to M?

A
mv2/2r
B
mv2rg
C
mv2g/r
D
mv2/rg

The tension in the string is due to the centripetal force of the mass = mv2/r

This is balanced by the weight of the mass Mg

∴Mg = mv2/r

so M = mv2/rg

 

Q13. What is the angular speed of a point on the Earth's equator?

A 7.3 × 10–5 rad s–1
B 4.2 × 10–3 rad s–1
C 2.6 × 10–1 rad s–1
D 15 rad s–1

 

Time for full rotation of 2π radians is 602 x 24 seconds

in one second: 2π/86400 = 7.27 x 10-5 radians/second

 

Q14. For a particle moving in a circle with uniform speed, which one of the following statements is correct?

A

The displacement of the particle is in the direction of the force.

No it isn't - the force is at right angles to the direction it travels - towards the centre of the circle. The particle is displaced at right angles to that.
B

The force on the particle is in the same direction as the direction of motion of the particle.

No it isn't - the force is at right angles to the direction it travels - towards the centre of the circle.
C

The momentum of the particle is constant.

Can't be - the velocity (well, the direction part of it) is constantly changing.
D

The kinetic energy of the particle is constant.

 

Q15. An object moving at constant speed in a circle experiences a force that is

A in the direction of motion.
B outwards and at right angles to the direction of motion.
C inwards and at right angles to the direction of motion.
D opposite to the direction of motion.

The force keeping an object moving in a circular path is the centripetal force.

It acts towards the centre of the circle - at right angles to the movement.

Q16. A ball of mass m, which is fixed to the end of a light string of length l, is released from rest at X. It swings in a circular path, passing through the lowest point Y at speed v.

If the tension in the string at Y is T, which one of the following equations represents a correct application of Newton's laws of motion to the ball at Y?

A
B
C
D

 

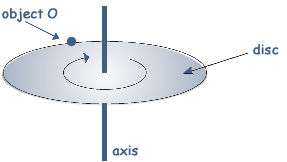
The tension in the string pulls at the mass. The centripetal force of the mass's circular motion is provided by the tension in the string. If we ignore weight then:

T = mv2/l

When it is in the position shown in the digram, the weight of the mass also produces tension in the string so

T = mv2/l + mg

This rearranges to give solution C.

Q17. A disc of diameter D is turning at a steady angular speed at frequency f about an axis through its centre.

What is the centripetal force on a small object O of mass m on the perimeter of the disc?

A
2πmfD
B
2πmf2D
C
2π2mf2D
D
2πmf2D2

 

acceleration = ω2r = ω2D/2

and ω = 2πf

So, a = 22Df2

F = ma

F= 22mf2D

Q18. What is the angular speed of a car wheel of diameter 0.400 m when the speed of the car is 108 kmh–1 ?

A
175 rad s–1
B
150 rad s–1
C
270 rad s–1
D
540 rad s–1

 

One turn of wheel makes the car travel π x 0.400 m.

Therefore the wheel turns:

108 x 103/ (π x 0.400) times in one hour and

108 x 103/ (π x 0.400 x 602) times in one second.

One complete turn is 2π radians, therefore in one second it turns:

108 x 103 x 2π / (π x 0.400 x 602)

= 216 x 103 / ( 0.400 x 602)

= 150 rads - choice B

 

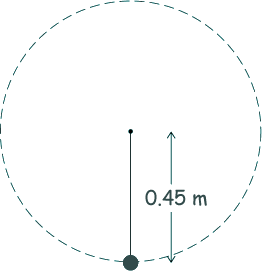
Q19. A bob of mass 0.50 kg is suspended from the end of a piece of string 0.45 m long.

The bob is rotated in a vertical circle at a constant rate of 120 revolutions per minute.

What is the tension in the string when the bob is at the bottom of the circle?

 

A
5.8 N
B
31 N
C
36 N
D
40 N

 

The tension in the string pulls at the mass, and so does gravity.

The centripetal force of the mass's circular motion is provided by the tension in the string.

If we ignore weight then:

T = mv2/r

When it is in the position shown in the digram, the weight of the mass also produces tension in the string so:

T = mv2/r + mg

Time for full rotation is 1/120 minutes

= 60/120 seconds

=0.5 seconds

So, in one second there are two revolutions

the circle perimeter is 2πr = 0.9π

∴ v = 1.8π m/s

T = 0.50 x (1.8π)2/0.45 + 0.5 x 9.81

T = (35.5 + 4.9)

T = 40.4 N (Choice D)