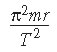Topic Menu

Cyber-chess a chess instruction site

Circular Motion - Multiple choice

Q1. A young child of mass 20 kg stands at the centre of a uniform horizontal platform which rotates at a constant angular speed of 3.0 rad s–1.

The child begins to walk radially outwards towards the edge of the platform. The maximum frictional force between the child and the platform is 200 N. What is the maximum distance from the centre of the platform to which the child could walk without the risk of slipping?

The frictional force must supply a force equal and opposite to the centripetal force for the child not to slip. Once it cannot equal that force she will fall.

mv2/r = m2r = 200

r =200/ m2 = 200/(20 x 3.02 ) = 10/9 = 1.1 m

A
1.1 m
B
1.3 m
C
1.5 m
D
1.7 m

 

 

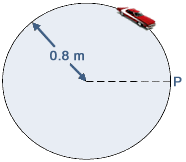
Q2. A model car moves in a circular path of radius 0.8 m at an angular speed of /2 rad s–1.

What is its displacement from point P, 6.0 s after passing P?

Full circle is 2π - therefore it takes 4 seconds to do one full cycle.

In 6 seconds it will have done one and a half.

It will therefore be directly opposite point P - a diameter away.

A
zero
B
1.6 m
C
0.4 m
D
1.6 m

 

Q3, What is the value of the angular velocity of a point on the surface of the Earth?

 

A 1.2 × 10–5 rad s–1
B 7.3 × 10–5 rad s–1
C 2.6 × 10–1 rad s–1
D 4.6 × 102 rad s–1

 

= v/r (data sheet)

distance travelled by a point on the Earth's surface in one day = 2r

time taken for that is 24 x 602s

Therefore velocity v = (2r)/(24 x 602)

= v/r = (2r)/(r x 24 x 602)

= (2)/(24 x 602) = 7.27 × 10–5 rad s–1

We didn't need the radius of the Earth at all as it cancelled - advantage of using symbols and not being too hasty to put numbers in!

But if you wanted it you can get it from your data sheet: the radius of the Earth is 6.37 x 106 m

 

Q4. A mass on the end of a string is whirled round in a horizontal circle at increasing speed until the string breaks. The subsequent path taken by the mass is:

A a straight line along a radius of the circle.
B a horizontal circle.
C a parabola in a horizontal plane.
D a parabola in a vertical plane.

 

When released it goes off at a tangent to the circle... as if it had been thrown horizontally.

Gravity affects its verical velocity - acceleration in the vertical direction; it goes at constant velocity in the horizontal direction.

It therefore follows a parabolic path when viewed in a verical plane.

 

Q5. A particle of mass m moves in a circle of radius r at uniform speed, taking time T for each revolution. What is the kinetic energy of the particle?

A
B
C
D

 

Length of path is 2πr during a time T, so the velocity is 2πr/T.

Kinetic energy is ½mv2 therefore you just substitute.

 

 

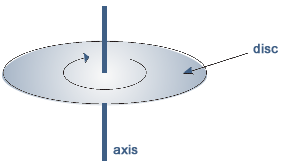
Q6. The diagram shows a disc of diameter 120 mm that can turn about an axis through its centre.

The disc is turned through an angle of 30° in 20 ms.

What is the average speed of a point on the edge of the disc during this time?

 

A
0.5 ms-1
B
ms-1
C
1.5 ms-1
D
2 ms-1

 

Always think first about the data you are given - and change it into the form you need to answer the question!

Angular velocity is measured in radians - therefore we need to change the 30o into radians.

360o = 2π rad

30o = π/6 rad

the time for it to turn 30o is given in millseconds for angular velocity we need to divide π/6 rad by 20 x 10-3s giving us 100 π/12

we are given a diameter of 120 mm - we need radius for the calculation - in metres!

r = 60 mm = 60 x 10-3 m

= v/r (data sheet)

so, v = r

v = 100 x 60 x 10-3/12

v = 0.5 ms-1

 

Q7. For a particle moving in a circle with uniform speed, which one of the following statements is correct?

A

The kinetic energy of the particle is constant.
B

The force on the particle is in the same direction as the direction of motion of the particle.

No it isn't - the force is at right angles to the direction it travels - towards the centre of the circle.
C

The momentum of the particle is constant.

Can't be - the velocity (well, the direction part of it) is constantly changing.
D

The displacement of the particle is in the direction of the force.

No it isn't - the force is at right angles to the direction it travels - towards the centre of the circle. The particle is displaced at right angles to that.

 

Q8. A particle travels at a constant speed around a circle of radius r with centripetal acceleration a.

What is the time taken for ten complete rotations?

Now, a = ω2r

Also note that T = time period = 1/f - and ω = 2πf = 2π/T

So, a = 42r/T2

and therefore T2 = 42r/a

and T= 2(r/a)

However - we want 10T = 20(r/a)

A
B
C
D

 

Q9. The wheel of the London Eye has a diameter of 130 m and can rotate at a steady speed, completing one rotation every 30 minutes.

What is the centripetal acceleration of a person in a capsule at the rim?

A 1.2 × 10–4 m s–2
B 2.5 × 10–4 m s–2
C 3.9 × 10–4 m s–2
D 7.9 × 10–4 m s–2

 

In 30 minutes it travels around a circular path - 2πr - you are given the diameter

r = 130/2 = 65 m

Speed = 2πr/(30 x 60) = 2π x 65 / 1800 = 0.227 ms-1

centripetal acceleration = v2/r

a = 0.2272/65

a = 7.9 x 10-4ms-1

 

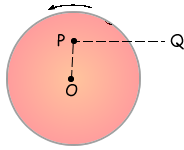
Q10. A small mass is placed at P on a horizontal disc which has centre O. The disc rotates anti-clockwise about a vertical axis through O with constant angular speed.

Which one of the following describes the force which keeps the mass at rest relative to the disc?

A the weight of the mass
B a frictional force directed away from O
C a frictional force directed towards O
D a frictional force directed from P to Q

 

Friction is the force that is is holding the mass in a circular path.

It therefore is acting towards the centre of the circle.