Topic Menu

Cyber-chess a chess instruction site

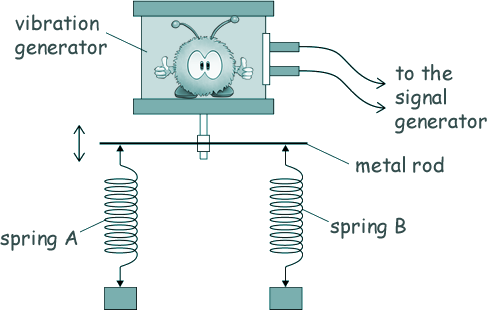
SHM - springs

Q6. A student is investigating forced vertical oscillations in springs.

Two springs, A and B, are suspended from a horizontal metal rod that is attached to a vibration generator.

The stiffness of A is k, and the stiffness of B is 3k.

Two equal masses are suspended from the springs as shown in the diagram below.

The vibration generator is connected to a signal generator.

The signal generator is used to vary the frequency of vibration of the metal rod.

When the signal generator is set at 2.0 Hz, the mass attached to spring A oscillates with a maximum amplitude of 2.5 × 10–2 m and has a maximum kinetic energy of 54 mJ.

(a) Deduce the spring constant k for spring A and the mass m suspended from it.

But ω = 2πf, so

x = 0 when v is a maximum

A = 2.5 × 10–2 m

f = 2.0 Hz

vmax=2π × 2.0 × 2.5 × 10-2

vmax= 0.314 m/s

EK = 54 × 10-3 J

EK = ½mv2

54 × 10-3 = ½m × 0.314 2

m = 2 x 54 × 10-3/0.314 2

= 1.1 kg

But T = 1/f, so

Squaring both sides

1/f2 = 4π2m/k

Rearranging to extract 'k':

k = 4π2mf2

k = 4π2 x 1.1 x 2.02

k = 174 N m-1

[4 marks]

(b) Calculate the frequency at which the mass attached to spring B oscillates with maximum amplitude.

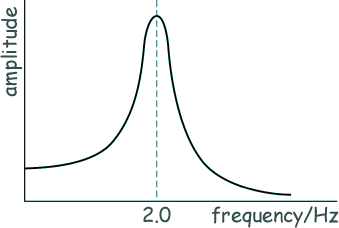
We have the same mass so f ∝ √k

∴frequency = 2.0 × √3

frequency = 3.5 Hz

[2 marks]

(c) The sketch graph indicates how the amplitude of the oscillations of the mass varies with frequency for spring A.

The investigation is repeated with the mass attached to spring B immersed in a beaker of oil. A graph of the variation of the amplitude with frequency for spring B is different from the sketch graph. Explain two differences that would be observed in the graph for spring B.

Any two factors with their reasoning from:

The resonance peak/maximum amplitude will be at a higher frequency due to the higher spring constant

The resonant peak would be broader due to damping

The amplitude would be lower (at all frequencies) due to energy losses from the system

[4 marks]

(Total 10 marks)