SHM - springs
Q3. A trolley of mass 0.80 kg rests on a horizontal surface attached to two identical stretched springs, as shown in the diagram. Each spring has a spring constant of 30 Nm–1, can be assumed to obey Hooke's law, and to remain in tension as the trolley moves.

(a)
(i) The trolley is displaced to the left by 60 mm and then released. Show that the magnitude of the resultant force on it at the moment of release is 3.6 N.
For one spring
change in force ΔF = kΔL
ΔF = 30 × 60 × 10–3
ΔF = 1.8 N 
Resultant force = [F + ΔF] – [F – ΔF]) = 2ΔF 
2ΔF = 2 x 1.8 = 3.6 N QED
(2 marks)
(ii) Calculate the acceleration of the trolley at the moment of release and state its direction.
F = ma
a = F/m = 3.6/0.8 = 4.5 ms–2 
to the right 
(2 marks)
(b)
(i) The oscillating trolley performs simple harmonic motion. State the two conditions which have to be satisfied to show that a body performs simple harmonic motion.
Acceleration is proportional to the displacement from the equilibrium position 
but acceleration is in the opposite direction to the displacement [or acceleration is always directed towards a fixed point/equilibrium position] 
(2 marks)
(ii) The frequency f of oscillation of the trolley is given by
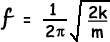
where
m = mass of the trolley
k = spring constant of one spring.
Calculate the period of oscillation of the trolley, stating an appropriate unit.
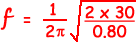

f = = 1.38 Hz
period T = 1/f = =1/1.38  = 0.72 s
= 0.72 s  (for the unit)
(for the unit)
(3 marks)
(c) Copper ions in a crystal lattice vibrate in a similar way to the trolley, because the inter-atomic forces act in a similar way to the forces exerted by the springs. The diagram below shows how this model of a vibrating ion can be represented.
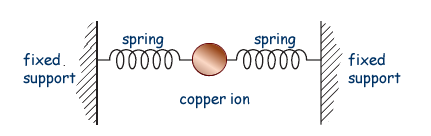
(i) The spring constant of each inter-atomic 'spring' is about 200 Nm–1. The mass of the copper ion is 1.0 × 10–25 kg. Show that the frequency of vibration of the copper ion is about 1013 Hz.
= 1.0 x 10-13 Hz QED
(1 mark)
(ii) If the amplitude of vibration of the copper ion is 10–11m, estimate its maximum speed.
vmax = 2πfA
vmax= 2π × 1013 × 10–11
vmax= 628 (3sf)
vmax= 630 ms–1 (2sf)
(1 mark)
(iii) Estimate the maximum kinetic energy of the copper ion.
max EK = ½ mvmax 2
max EK= ½ × 1.0 × 10–25 × 6282
max EK= 2.0 × 10–20 J 
(1 mark)
(Total 12 marks)








