Topic Menu

Cyber-chess a chess instruction site

SHM - springs

Q2. A simple model for the suspension system of a car represents the car as a rectangular block, the weight of which is supported equally by four identical springs that are fixed rigidly at their lower ends, as shown in the diagram.

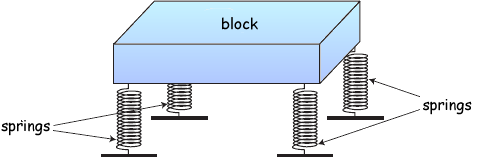
(a) The mass of the block is 1600 kg, and tests have shown that vertical oscillations of the block have a frequency of 0.92 Hz. Calculate the spring constant of one of the springs.

We are given the frequency - therefore we need to use T = 1/f = 1/0.92 so that we can put the value into the spring equation.

ONE spring supports a quarter of the total mass - 1600/4 = 400 kg

k = 1.3(4) × 104 N m-1

[or you can do it by the use of an effective spring constant for all four springs: springs in parallel so k’ = 4k for a total mass of 1600 kg]

(2 marks)

(b) In a further test of the model, the whole block is displaced vertically downwards with an initial displacement of 90 mm. The block is then released at time t = 0.

You may assume that subsequently the block oscillates vertically with undamped simple harmonic motion.

Calculate, for a time 0.20 s later,

(i) the vertical displacement of the block from its equilibrium position,

when t = 0.20 s

x = A cos 2π ft

x = 90 cos 2π (0.92 × 0.20)

x = 36(.3) mm

downwards

(ii) the vertical speed of the block.

v = 0.47(6) m s-1

[or v = (-2π fA sin 2πft) = (-) 2π × 0.92 × 90 × 10-3 sin (2π × 0.92 × 0.20)]

(4 marks maximum)

(c) In practice, the vertical oscillations of a car are greatly reduced by fitting dampers (known as shock absorbers) to the suspension system. The graph below shows how displacement against time would appear if there were no damping. Draw a graph on the axes beneath it to show how the oscillations would vary with time for a car fitted with light damping.

You should use the same time scale.

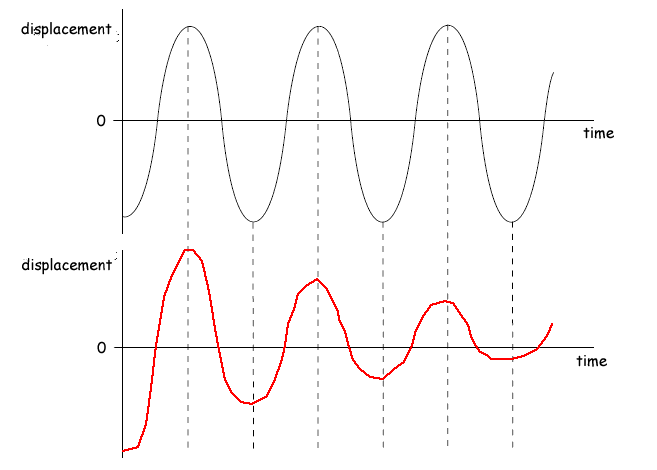
same period maintained throughout graph

exponential decay of amplitude

(2 marks)

(d) An experiment is carried out to investigate the rattling of internal components of a car at certain engine speeds. When a loudspeaker connected to an ac source of variable frequency is placed in front of the rear-view mirror, violent vibrations of the mirror are produced when the frequency of the sound waves is 55 Hz.

(i) Give the name of this phenomenon.

resonance

(ii) Deduce the engine speed, in revolutions per minute, at which the same effect would be likely to occur in the car.

55 Hz requires 55 rev per second to resonate

= 55 x 60

= 3300 rev min-1

(2 marks)

(10 marks Total)