SHM - springs
Q1
(a) A body is moving with simple harmonic motion. State two conditions that must be satisfied concerning the acceleration of the body.
For a body to be moving with simple harmonic motion acceleration must be:
- proportional to displacement

- in the opposite direction to displacement, OR always acting towards a fixed point, or towards the centre of oscillation

(2 marks)
(b) A mass is suspended from a vertical spring and the system is allowed to come to rest. When the mass is now pulled down a distance of 76 mm and released, the time taken for 25 oscillations is 23 s.
Calculate
frequency = 25/23 = 1.09
f = 1.1 Hz 
(ii) the maximum acceleration of the mass,
a = (2πf)2A
a = (2π × 1.09)2 × 76 × 10−3 
a = 3.6 m s−2 
(iii) the displacement of the mass from its rest position 0.60 s after being released. State the direction of this displacement.
x = A cos (2πft)
x = 76 × 10−3 cos (2π × 1.09 × 0.60) 
x = − 4.3 × 10−2 m 
x = 43 mm
direction: above equilibrium position or upwards 
(6 marks)
(c)The diagram below shows qualitatively how the velocity of the mass varies with time over the first two cycles after release.
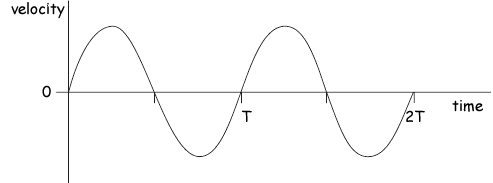
(i) Using the axes below, sketch a graph to show qualitatively how the displacement of the mass varies with time during the same time interval.
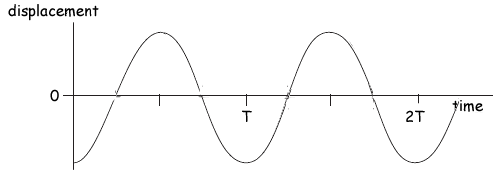
correct shape, i.e. cos curve 
correct phase i.e. −(cos) 
(ii) Using the axes in below sketch a graph to show qualitatively how the potential energy of the mass-spring system varies with time during the same time interval.
graph to show:
two cycles per oscillation 
correct shape (even if phase is wrong) 
correct starting point 
(4 marks)
(Total 12 marks)


