Q1.

(a) Describe the energy changes that take place as the bob of a simple pendulum makes one complete oscillation, starting at its maximum displacement.

Starting at maximum displacement it has maximum gravitational potential energy and no kinetic energy. As it swings towards the equilibrium poinsition the gravitational potential energy changes into kinetic energy . By the time it reaches the midpoint of the swing all of the energy is in the form of kinetic energy. As it swings out to the other extreme position the kinetic energy changes into gravitational potential energy. This then converts to kinetic energy as it swings back to the mid-point of the path. As it returns to the original position, the kinetic energy changes back to gravitational potential energy again.

To get this mark you have to describe the changes from GPE to KE to GPE to KE and back to GPE again - they ask for oe complete oscillation.

During this repetative energy change between GPE and KE, energy is lost to surroundings as heat energy in overcoming air resistance and friction at the pivot point.

(2 marks)

The diagram shows a young girl swinging on a garden swing.

You may assume that the swing behaves as a simple pendulum. Ignore the mass of chains supporting the seat throughout this question, and assume that the effect of air resistance is negligible.

15 complete oscillations of the swing took 42s.

(b)

(i) Calculate the distance from the top of the chains to the centre of mass of the girl and seat. Express your answer to an appropriate number of significant figures.

We have to find the length of the pendulum.

Period T = ⁴²/₁₅ = 2.8 s

T² = 4²L/g

L = T²g/4²

= 2.8² x 9.81 /4²

= 1.95 m (3sf) This value is 1.9482 rounded to give 3sf. If we need to use this length in later parts of the question, this value is the one we would use. You therefore need to have a value at one more than the final required sig fig answer.

= 1.9 m The values in the question are to 2sf - the final answer should therefore be 2sf - for that extra mark. The examiners allow you to be one more than that... but not one less. NEVER give answers to 1 sf!!!

(4 marks)

(ii) To set her swinging, the girl and seat were displaced from equilibrium and released from rest. This initial displacement of the girl raised the centre of mass of the girl and seat 250 mm above its lowest position. If the mass of the girl was 18 kg, what was her kinetic energy as she first passed through this lowest point?

At starting point all energy is gravitational potential.

mgh = 18 x 9.81 x 0.250 = 44.1 J

This energy is transferred into kinetic energy by the centre of the swing so the kinetic energy of the girl at the lowest point is 44 J

(2 marks)

(iii) Calculate the maximum speed of the girl during the first oscillation.

Maximum speed is at the lowest point

E_k = ¹/₂ mv² = 44.1

v² = 2 x ^44.1/₁₈ = 4.9

v = 2.2 m s^-1

(1 mark)

(c)

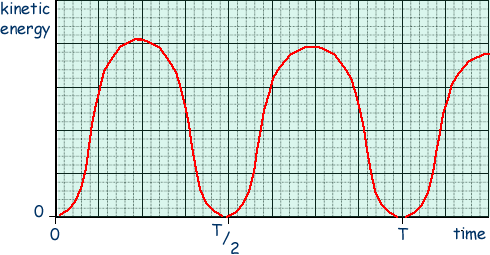
On the diagram above draw a graph to show how the kinetic energy of the girl varied with time during the first complete oscillation, starting at the time of her release from maximum displacement. On the horizontal axis of the graph, T represents the period of the swing. You do not need to show any values on the vertical axis.

One mark for the general shape

The kinetic energy varies in the form of a sin² function shape - which looks a lot like a sine curve!

This is because E_k = ¹/₂ mv² = constant x v².

At time t = 0s ^T/₂ and T the swing is stationary, therefore

One mark for making E_k zero when t = 0s, ^T/₂ and T

The transfer of energy from GPE to KE will involve a samll loss from the system as heat at friction point. Therefore therewill be slight attenuation of the graph trace (maxima will gradually diminish). This would not be very noticable for a couple of swings.

One mark if their is slight attenuation or if the maxima are equal height.

(3 marks)

(Total 12 marks)