Simple Harmonic Motion - Multiple Choice Questions

Q21. A particle of mass m oscillates in a straight line with simple harmonic motion of constant amplitude.

The total energy of the particle is E.

What is the total energy of another particle of mass 2m, oscillating with simple harmonic motion of the same amplitude but double the frequency?

Total energy = maximum KE = maximum PE

KE_max =¹/₂ mv_max²

KE_max = 0.5 x m (2πfA)²

KE_maxis ∝to mf²

therefore the new particle will have energy x 2 (for mass doubling) and x 2² (for frequency doubling)

a multiplication factor of 2 x 4 = 8

∴ the answer is choice D

Q22. When a mass suspended on a spring is displaced, the system oscillates with simple harmonic motion.

Which one of the following statements regarding the energy of the system is incorrect?

A	The potential energy has a minimum value when the spring is fully compressed or fully extended.
B	The kinetic energy has a maximum value at the equilibrium position.
C	The sum of the kinetic and potential energies at any time is constant.
D	The potential energy has a maximum value when the mass is at rest.

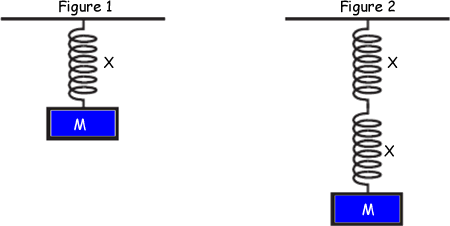
Q23. When a mass M attached to a spring X, as shown in Figure 1, is displaced downwards and released it oscillates with time period T.

An identical spring is connected in series and the same mass M is attached, as shown in figure 2.

What is the new time period?

Putting the springs in series halves k (stretch of the system doubles for a given mass)

T₁√k ₁= T₂√k ₂

T₂ = T₁√(k ₁/k ₂)

T₂ = T√2 - choice C

Q24. Which graph best shows how the kinetic energy of a simple pendulum varies with displacement from the equilibrium position?

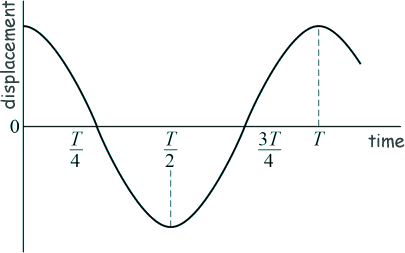
The kinetic energy at the extremes is zero and a maximum in the centre - so the answer must be A or D.

Speed changes most rapidly at the extremes but not uniformly as it accelerates towards the centre acceleration decreases - so it must be D

Q25. The sketch-graph below shows how the displacement of a particle performing simple harmonic motion varies with time.

Which statement is not correct?

A	The speed of the particle is a maximum at time ¼T True - speed is a max when displacement is zero
B	The potential energy of the particle is zero at time ¾T True - speed (and KE) is a max when displacement is zero and PE is zero
C	The acceleration of the particle is a maximum at time ½T True - maximum change in velocity happens at the extremes of the swing.
D	The restoring force acting on the particle is zero at time T Untrue - held out to the side of the equilibrium position the restoring force acts on it.